题目内容
如图①,直角梯形ABCD中,动点P从B点出发,由B-C-D-A沿 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为16
16
.分析:解本题需注意一定的面积值相对应的距离可以有2个.找到对应的点,找出准确反映y与x之间对应关系的图象,需分析在不同阶段中y随x变化的情况.
解答:解:由图2知:当x=4和x=9时,△ABP的面积相等,
∴BC=4,BC+CD=9,
即CD=5,又知AD=5,
∴在直角梯形ABCD中AD=5,
如图,作DE⊥AB,
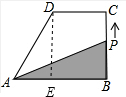
∵∠B=90°
∴DE=BC=4,在直角△AED中:AE=
=
=3,
∴AB=AE+EB=3+5=8,
∴S△ABC=
AB×BC=
×8×4=16.
故答案为16.
∴BC=4,BC+CD=9,
即CD=5,又知AD=5,
∴在直角梯形ABCD中AD=5,
如图,作DE⊥AB,

∵∠B=90°
∴DE=BC=4,在直角△AED中:AE=
| AD2-DE2 |
| 25-16 |
∴AB=AE+EB=3+5=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为16.
点评:考查了动点问题的函数图象,解决本题的关键是读懂图意,得到相应的直角梯形中各边之间的关系.此题考查了学生从图象中读取信息的数形结合能力.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
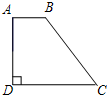 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
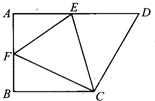 12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=
12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF= 为t(单位:秒).
为t(单位:秒). (2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( )
(2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( ) 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究:
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究: