题目内容
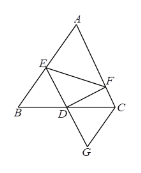
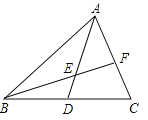
【题目】如图,已知AD是△ABC的中线,E是AD上的一点,且AE=2DE,连接BE并延长交AC于点F.
(1)求证:AF=FC;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)3.
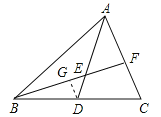
【解析】(1)过D作DG∥AC交BF于点G,则DG是△BCF的中位线,且△DEG∽△AEF,依据三角形中位线定理以及相似三角形的性质,确定AF、FC与DG的关系即可证得;
(2)根据(1)中△DEG∽△AEF,DG是△BCF的中位线,利用EF表示出BF即可.
(1)过D作DG∥AC交BF于点G.
∵DG∥AC,又AD是△ABC的中线,即BD=DC,∴DG=![]() FC.
FC.
∵DG∥AC,∴△DEG∽△AEF,∴![]() =
=![]() .又∵AE=2DE,∴
.又∵AE=2DE,∴![]() =
=![]() ,则DG=
,则DG=![]() AF,∴AF=FC;
AF,∴AF=FC;
(2)∵DG∥AC,又AD是△ABC的中线,即BD=DC,∴BF=2GF.
∵△DEG∽△AEF,∴![]() =
=![]() =
=![]() ,∴GE=
,∴GE=![]() EF,设EF=2x,则GE=x,GF=3x,∴BF=2GF=6x,则
EF,设EF=2x,则GE=x,GF=3x,∴BF=2GF=6x,则![]() =
=![]() =3.
=3.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
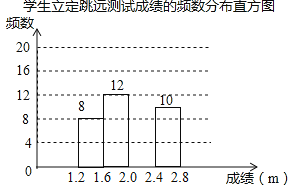
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?