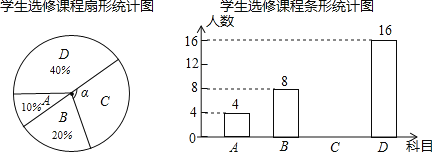
题目内容
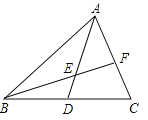
【题目】如图,在△ABC中,D为BC的中点,E为AB上一点,DF⊥DE交AC于点F,延长ED至点G,使GD=ED,连接CG.
(1)求证:BE=CG;
(2)求证:BE+CF>EF.
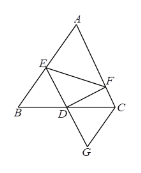
【答案】(1)见解析;(2)见解析.
【解析】
(1)由点D为BC的中点,ED=GD,利用SAS,即可判定△BDE≌△CDG,又由全等三角对应边相等,证得BE=CG.
(2)首先连接FG,由线段垂直平分线的性质,可证得EF=FG,结合BE=CG,由三角形三边关系,即可证得结论.
解: (1) 在△BDE和△CDG中,
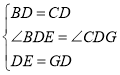 ,
,
∴△BDE≌△CDG (SAS),
∴BE=CG;
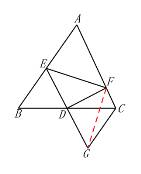
(2) 连接FG
∵ED=GD,DF⊥DE,
∴EF=GF,
在△CFG中, CF+CG>GF,
∵BE=CG,
∴BE+CF>EF.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目