题目内容
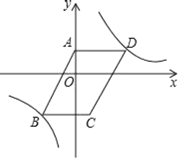
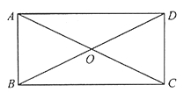
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
【答案】(1)证明见解析;(2)∠ADO==36°.
【解析】
(1)先判断四边形ABCD是平行四边形,继而根据已知条件推导出AC=BD,然后根据对角线相等的平行四边形是矩形即可;
(2)设∠AOB=4x,∠ODC=3x,则∠OCD=∠ODC=3x.,在△ODC中,利用三角形内角和定理求出x的值,继而求得∠ODC的度数,由此即可求得答案.
(1)∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
又∵∠AOB=2∠OAD,∠AOB是△AOD的外角,
∴∠AOB=∠OAD+∠ADO.
∴∠OAD=∠ADO.
∴AO=OD.
又∵AC=AO+OC=2AO,BD=BO+OD=2OD,
∴AC=BD.
∴四边形ABCD是矩形.
(2)设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x,
在△ODC中,∠DOC+∠OCD+∠CDO=180°
∴4x+3x+3x=180°,解得x=18°,
∴∠ODC=3×18°=54°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO=∠ADC-∠ODC=90°-54°=36°.

练习册系列答案
相关题目
【题目】下列表格是某学校女子排球队队员年龄统计表:
年龄(岁) | 13 | 14 | 15 | 16 |
人数(人) | 1 | 2 | 4 | 5 |
(1)该排球队队员年龄的众数是 岁;
(2)事件“从该排球队随机选择一名队员,其年龄为13岁”发生的概率为 ;
(3)教练決定从年龄为13岁和14岁的A、B、C三名队员中,随机选取两名队员进行“接发球”训练,求队员A、B同时被选中的概率.(树状图或列表法)