题目内容
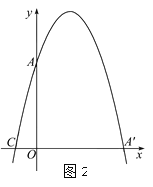
【题目】在平面直角坐标系中，平行四边形ABOC如图放置，点A、C的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．
（1）若抛物线经过点C、A、A′，求此抛物线的解析式；
（2）点M时第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；
（3）若P为抛物线上一动点，N为x轴上的一动点，点Q坐标为（1，0），当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．
【答案】（1）y＝－x2＋3x＋4；（2）△AMA′的面积最大S△AMA′＝8，M（2，6）；（3）当P1（0，4），P2（3，4），P3（
,－4），P4（
，－4）时，P、N、B、Q构成平行四边形；当这个平行四边形为矩形时，N1（0，0），N2（3，0）.
【解析】试题分析：（1）先由OA′＝OA得到点A′的坐标，再用点C、A、A′的坐标即可求此抛物线的解析式；（2）连接AA′, 过点M 作MN⊥x轴，交AA′于点N,把△AMA′分割为△AMN和△A′MN, △AMA′的面积＝△AMA′的面积＋△AMN的面积＝
OA′MN,设点M的横坐标为x，借助抛物线的解析式和AA′的解析式，建立MN的长关于x的函数关系式，再据此建立△AMA′的面积关于x的二次函数关系式，再求△AMA′面积的最大值以及此时M的坐标；（3）在P、N、B、Q 这四个点中，B、Q 这两个点是固定点，因此可以考虑将BQ作为边、将BQ作为对角线分别构造符合题意的图形，再求解.
试题解析：（1）∵平行四边形ABOC绕点O顺时针旋转90°，得到平行四边形A′B′OC′，点A的坐标是（0，4），∴点A′的坐标为（4，0），点B的坐标为（1，4）.
∵抛物线过点C，A，A′，设抛物线的函数解析式为y＝ax2＋bx＋c（a≠0）,可得：
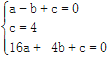. 解得：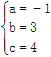
.∴抛物线的函数解析式为y＝－x2＋3x＋4.
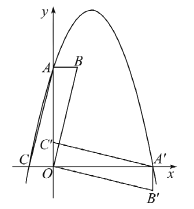
（2）连接AA′，设直线AA′的函数解析式为y＝kx＋b，可得
.解得：
.
∴直线AA'的函数解析式是y＝－x＋4.
设M（x，－x2＋3x＋4），
S△AMA′＝×4×[－x2＋3x＋4一（一x＋4）]＝一2x2＋8x＝一2（x－2）2＋8.
∴x＝2时，△AMA′的面积最大S△AMA′＝8．
∴M（2，6）.
（3）设P点的坐标为（x，－x2＋3x＋4），当P、N、B、Q构成平行四边形时，
①当BQ为边时，PN∥BQ且PN＝BQ，
∵BQ＝4，∴一x2＋3x＋4＝±4.
当一x2＋3x＋4＝4时，x1＝0，x2＝3，即P1（0,4），P2（3，4）；
当一x2＋3x＋4＝一4时，x3＝，x4＝，即P3（,－4），P4（，－4）；
②当BQ为对角线时，PB∥x轴，即P1（0，4），P2（3，4）;
当这个平行四边形为矩形时，即Pl（0，4），P2（3，4）时，N1（0，0），N2（3，0）.
综上所述，当P1（0，4），P2（3，4），P3（,－4），P4（，－4）时，P、N、B、Q构成平行四边形；当这个平行四边形为矩形时，N1（0，0），N2（3，0）.
