题目内容
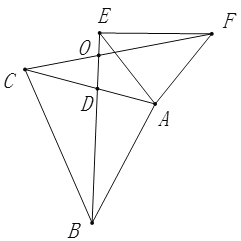
【题目】如图,E、F、 G、H分别为四边形ABCD四边之中点.
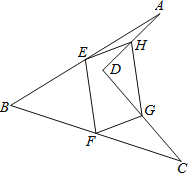
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足______时,四边形EFGH为矩形.
【答案】(1)见解析;(2)AC⊥BD
【解析】
(1)连接BD,根据中位线的性质可得EH∥BD,EH=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() ,从而得出EH∥FG,EH= FG,然后根据平行四边形的判定定理即可证出结论;
,从而得出EH∥FG,EH= FG,然后根据平行四边形的判定定理即可证出结论;
(2)当AC⊥BD时,连接AC,根据中位线的性质可得EF∥AC,从而得出EF⊥BD,然后由(1)的结论可证出EF⊥EH,最后根据有一个角是直角的平行四边形是矩形即可证出结论.
(1)证明:连接BD
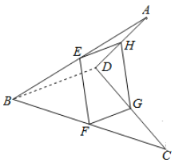
∵E、F、 G、H分别为四边形ABCD四边的中点
∴EH是△ABD的中位线,FG是△CBD的中位线
∴EH∥BD,EH=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]()
∴EH∥FG,EH= FG
∴四边形EFGH为平行四边形;
(2)当AC⊥BD时,四边形EFGH为矩形,理由如下
连接AC,
∵E、F为BA和BC的中点
∴EF为△BAC的中位线
∴EF∥AC
∵AC⊥BD
∴EF⊥BD
∵EH∥BD
∴EF⊥EH
∴∠FEH=90°
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形
故答案为:AC⊥BD.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目