题目内容
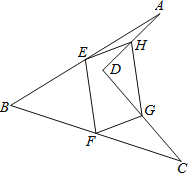
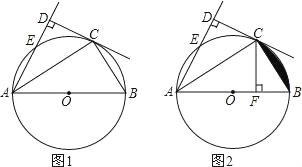
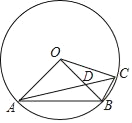
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
【答案】(1) 30°;(2) 弧BC, ![]() .
.
【解析】
(1)作OF⊥AC于F,如图,设CD=x,则AD=2x,利用等腰三角形性质得AF=![]() x,则DF=
x,则DF=![]() x,再证明△AOF∽△ODF,利用相似比得到OF=
x,再证明△AOF∽△ODF,利用相似比得到OF=![]() x,则利用三角函数可求出∠OAF=30°,从而得到∠BOC的度数;
x,则利用三角函数可求出∠OAF=30°,从而得到∠BOC的度数;
(2)利用含30度的直角三角形三边的关系得到OF=1,AF=![]() ,则AC=2
,则AC=2![]() ,所以CD=
,所以CD=![]() ,然后根据三角形面积公式和扇形面积公式,利用线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC-S△ODC进行计算.
,然后根据三角形面积公式和扇形面积公式,利用线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC-S△ODC进行计算.
解:(1)作OF⊥AC于F,如图,设CD=x,则AD=2x,
∵OA=OC,
∴AF=![]() AC=
AC=![]() x,
x,
∴DF=2x﹣![]() x=
x=![]() x,
x,
∵OA⊥OB,
∴∠AOB=90°,
∴△AOF∽△ODF,
∴OF2=AFDF=![]() x
x![]() x,
x,
∴OF=![]() x,
x,
在Rt△OAF中,tan∠OAF=![]() =
=![]() =
=![]() ,
,
∴∠OAF=30°,
∴∠AOC=120°,
∴∠BOC=120°﹣90°=30°;
(2)∵OA=2,
∴OF=1,AF=![]() ,
,
∴AC=2![]() ,
,
∴CD=![]() AC=
AC=![]() ,
,
∴线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC﹣S△ODC=![]() ﹣
﹣![]()
![]() 1=
1=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目