题目内容
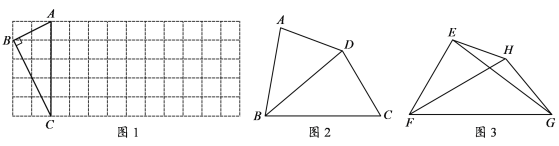
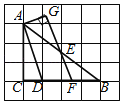
【题目】如图，在网格纸中，每个小正方形的边长都是1个单位长度，每个小正方形的顶点叫做格点，点A，B，C，D均落在格点上，点E是AB的中点，过点E作EF∥AD，交BC于点F，作AG⊥EF，交FE延长线于点G，则线段EG的长度是_____．
【答案】
．
【解析】
如图，作DJ⊥AB于J．解直角三角形求出AD，AJ，DJ，再证明△AJD∽△EGA，可得
＝
，由此即可解决问题．
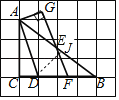
解：如图，作DJ⊥AB于J．
在Rt△ACB中，∵AC＝3，BC＝4，∠C＝90°，
∴AB＝
＝
＝5，
∵S△ABD＝
×3×3＝×AB×DJ，
∴DJ＝
，
∵AD＝
＝
＝
，
∴AJ＝
＝
＝
，
∵AG⊥EG，
∴∠G＝∠AJD＝90°，
∵AD∥EG，
∴∠DAJ＝∠AEG，
∴△AJD∽△EGA，
∴＝，
∴
＝
，
∴EG＝，
故答案为．
练习册系列答案
相关题目
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让学生进行摸球试验，每次摸出一个球（放回），下表是活动进行中的一组统计数据．
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
（1）
= ，根据上表数据估计从袋中摸出一个黑球的概率是 ．
（2）估算袋中白球的个数为 ．
（3）在（2）的条件下，若小强同学从袋中摸出两个球，用画树状图或列表的方法计算摸出的两个球都是白球的概率．
