题目内容
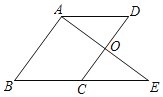
【题目】如图：在矩形ABCD中，AB＝1．BC＝
，P为边AD上任意一点，连接PB，则PB+
PD的最小值为（ ）
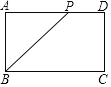
A.
B.2C.D.
【答案】C
【解析】
连接BD，根据矩形ABCD中，AB＝DC＝1．BC＝
，可得tan∠DBC＝
，得∠DBC＝30°，作∠DBN＝∠DBC＝30°，过点D作DM⊥BN于点M，BN交AD于点P，此时BP+
PD＝BP+PM最小，最小值为BM的长．
连接BD，
在矩形ABCD中，AB＝DC＝1，BC＝，
∴tan∠DBC＝
＝，
∴∠DBC＝30°
作∠DBN＝∠DBC＝30°，
过点D作DM⊥BN于点M，BN交AD于点P．
∴∠MDB＝60°，
∵AD∥BC
∴∠PDB＝∠DBC＝30°，
∴∠MDP＝30°，
∴PM＝PD，
此时，BP+PD的最小值＝BP+PM=BM，
∵∠MBD＝∠CBD，∠BMD＝∠C＝90°，BD＝BD
∴△BMD≌△BCD（AAS），
∴BM＝BC＝，
答：PB+PD的最小值为．
故选：C．
练习册系列答案
相关题目
