题目内容
【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】连接OB,根据点O是为对角线AC的中点可得△ABO和△BOC的面积相等,又点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,然后把开始时、结束时、与中点时的△OPQ的面积与△ABC的面积相比即可进行判断.
解:如图所示,
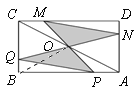
连接OB,∵O是AC的中点,
∴S△ABO=S△BOC=![]() S△ABC,
S△ABC,
开始时,S△OBP=S△AOB=![]() S△ABC,
S△ABC,
点P到达AC的中点时,点Q到达BC的中点时,S△OPQ=![]() S△ABC,
S△ABC,
结束时,S△OPQ=S△BOC=![]() S△ABC,
S△ABC,
所以,图中阴影部分面积的大小变化情况是:先减小后增大.
故选C.
“点睛“本题考查了动点问题的函数图象,根据题意找出关键的开始时,中点时,结束时三个时间点的三角形的面积与△ABC的面积的关系是解题的关键.

练习册系列答案
相关题目




