题目内容
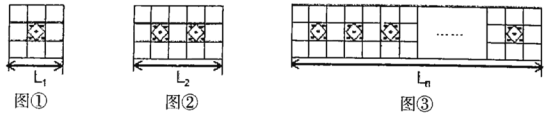
【题目】如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.5m.
(1)按图示规律,第一图案的长度L1= m;第二个图案的长度L2= m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系;
(3)当走廊的长度L为20.5m时,请计算出所需带有花纹图案的瓷砖的块数,
【答案】(1)1.5,2.5;(2)L=(2n+1)×0.5;(3)需要20个有花纹的图案.
【解析】
(1)观察题目中的已知图形,可得前两个图案中有花纹的地面砖分别有:1,2个,第二个图案比第一个图案多1个有花纹的地面砖,所以可得第n个图案有花纹的地面砖有n块;第一个图案边长3×0.5=L,第二个图案边长5×0.5=L,
(2)由(1)得出则第n个图案边长为L=(2n+1)×0.5;
(3)根据(2)中的代数式,把L为20.5代入求出n的值即可.
解:(1)第一图案的长度:L1=0.5×3=1.5,第二个图案的长度:L2=0.5×5=2.5;
故答案为:1.5,2.5;
(2)观察可得:第1个图案中有花纹的地面砖有1块,第2个图案中有花纹的地面砖有2块,…故第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.5,第二个图案边长L=5×0.5,
则第n个图案边长为:L=(2n+1)×0.5;
(3)把L=20.5代入L=(2n+1)×0.5中得:
20.5=(2n+1)×0.5,
解得:n=20,
答:需要20个有花纹的图案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目