题目内容
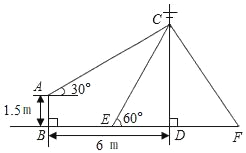
【题目】如图所示的方格纸中，每小方格的边长都为1.请在方格纸上画图并回容问题：已知点A、B.
(1)画直线AB，射线BC；
(2)过点C作垂线段CD⊥AB，垂足为点D.
(3)连结AC，则△ABC的面积＝_______.
(4)已知AB=5，求线段CD的长.
【答案】（1）（2）见解析（3）6；（4）
.
【解析】
（1）根据图形即可作出直线AB,射线BC；
（2）根据垂线的定义即可作出；
（3）根据网格的长度及三角形的面积公式即可写出；
（4）根据等面积法即可求出斜边上的高.
（1）如图，直线AB,射线BC为所求；
（2）线段CD为所求；
（3）△ABC的面积=
BC×AC=×3×4=6，
故填：6；
（4）∵△ABC的面积=BC×AC=AB×CD
∴CD=
=.
【题目】“十一”期间，某风景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数，负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 单位：万人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人数记为
，请用含的代数式表示10月2日的游客人数？
(2)请判断七天内游客人数最多的是哪天？请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处；另一方面拉动了内需，促进了消费.若9月30日的游客人数为1万人，进园的人每人平均消费60元，问“十一”期间所有游园人员在此风景区的总消费是多少元？(用科学记数法表示)
【题目】某商场计划经销A、B两种新型节能台灯共50盏，这两种台灯的进价、售价如下表所示．
A型 | B型 | |
进价（元/盏） | 40 | 65 |
售价（元/盏） | 60 | 100 |
（1）若该商场购进这批台灯共用去2500元，问这两种台灯各购进多少盏？
（2）在每种台灯销售利润不变的情况下，若该商场销售这批台灯的总利润不少于1400元，问至少需购进B种台灯多少盏？
（3）若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯，为了打开B种台灯的销路，商场决定每售出一盏B种台灯，返还顾客现金a元（10＜a＜20），问该商场该如何进货，才能获得最大的利润？