题目内容
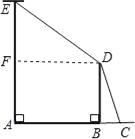
【题目】如图，AE是位于公路边的电线杆，为了使拉线CDE不影响汽车的正常行驶，电力部门在公路的另一边竖立了一根水泥撑杆BD，用于撑起拉线．已知公路的宽AB为8米，电线杆AE的高为12米，水泥撑杆BD高为6米，拉线CD与水平线AC的夹角为67.4°．求拉线CDE的总长L（A、B、C三点在同一直线上，电线杆、水泥杆的大小忽略不计）．（参考数据：sin67.4°≈
，cos67.4°≈
，tan67.4°≈
）
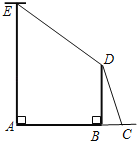
【答案】16.5
【解析】试题分析：根据sin∠DCB=
，得出CD的长，再根据矩形的性质得出DF=AB=8，AF=BD=6，进而得出拉线CDE的总长L．
试题解析：在Rt△DBC中，sin∠DCB=，
∴CD=
=6.5（m）．
作DF⊥AE于F，则四边形ABDF为矩形，
∴DF=AB=8，AF=BD=6，
∴EF=AE﹣AF=6，
在Rt△EFD中，ED=
=10（m）．
∴L=10+6.5=16.5（m）
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
【题目】在学校组织的社会实践活动中，甲、乙两人参加了射击比赛，每人射击七次，命中的环数如表：
序号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
甲命中的环数（环） | 7 | 8 | 8 | 6 | 9 | 8 | 10 |
乙命中的环数（环） | 5 | 10 | 6 | 7 | 8 | 10 | 10 |
根据以上信息，解决以下问题：
（1）写出甲、乙两人命中环数的众数；
（2）已知通过计算器求得 
=8， 
≈1.43，试比较甲、乙两人谁的成绩更稳定？
