��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У��������¶��壺����y=��x��m����x��m+1����y=��x��m����x��m��1�����������κ�����ͼ������ֵ������ߣ�
��1����д��һ���ֵ������ߵĽ���ʽ��
��2�������κ���y=x2��x��ͼ����ͼ����y=x2��bx+2��ͼ�����ֵ������ߣ�
����b��ֵ��
����ֱ��y=k������ֵ����������ĸ����㣬������������ΪA��B��C��D�ĸ��㣬����B����CΪ�߶�AD���ȷֵ㣬���߶�BC�ij���
���𰸡���1����m=0����y=��x��m����x��m+1����y=��x��m����x��m��1�������ɵõ�һ���ֵ�������
��2����y=x2��x=x��x��1����������������ۣ�
���һ����y=x��x��1��������y=��x��m����x��m+1�������m=1���õ���һ����������ʽ�������ó�b��ֵ��
���������y=x��x��1��������y=��x��m����x��m��1����ͬ����⣻
�������������������1����m=0����y=��x��m����x��m+1����y=��x��m����x��m��1�������ɵõ�һ���ֵ������ߣ�
��2����y=x2��x=x��x��1����������������ۣ�
���һ����y=x��x��1��������y=��x��m����x��m+1�������m=1���õ���һ����������ʽ�������ó�b��ֵ��
���������y=x��x��1��������y=��x��m����x��m��1����ͬ����⣻
������ƽ�ƵĹ��ɿ�֪��y=x2��3x+2��ͼ����Կ�������y=x2��x��ͼ������ƽ��1����λ�õ�����������������k��0�����A���B��ƽ�ƶ�Ӧ�㣬AB=1���ٸ������ȷֵ�Ķ��弴����⣻���k��0�����A���C��ƽ�ƶ�Ӧ�㣬AC=1��ͬ����⼴�ɣ�
���������
��1����m=0ʱ���õ�һ���ֵ������ߣ�
y=x��x+1����y=x��x��1����
��2����y=x2��x=x��x��1����
���һ����y=x��x��1��������y=��x��m����x��m+1������m=1������һ������Ϊy=��x��1����x��2������y=x2��3x+2��b=3��
���������y=x��x��1��������y=��x��m����x��m��1������m=0������һ������Ϊy=x��x��1������y=x2��x������֪ì�ܣ�
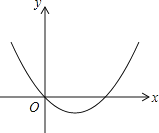
��y=x2��3x+2��ͼ����Կ�������y=x2��x��ͼ������ƽ��1����λ�õ�����ͼ��
���k��0�����A���B��ƽ�ƶ�Ӧ�㣬AB=1��
����B����CΪ�߶�AD���ȷֵ㣬
��AB=BC=CD=![]() AD=1����BC=1��
AD=1����BC=1��
���k��0�����A���C��ƽ�ƶ�Ӧ�㣬AC=1��
����B����CΪ�߶�AD���ȷֵ㣬
��AB=BC=![]() AC=
AC=![]() ����BC=
����BC=![]() ��
��
���߶�BC�ij�Ϊ1��![]() ��
��


 �������ϵ�д�
�������ϵ�д�