题目内容
【题目】如图,在四边形ACBD中,AC=6,BC=8,AD=2![]() ,BD=4
,BD=4![]() ,DE是△ABD的边AB上的高,且DE=4,求△ABC的边AB上的高.
,DE是△ABD的边AB上的高,且DE=4,求△ABC的边AB上的高.
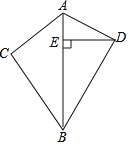
【答案】△ABC的边AB上的高为4.8.
【解析】
先根据勾股定理求出AE和BE,求出AB,根据勾股定理的逆定理求出△ABC是直角三角形,再求出面积,进一步得到△ABC的边AB上的高即可.
∵DE是AB边上的高,
∴∠AED=∠BED=90°,
在Rt△ADE中,
由勾股定理,得AE=![]() .
.
同理:在Rt△BDE中,由勾股定理得:BE=8,
∴AB=2+8=10,
在△ABC中,由AB=10,AC=6,BC=8,
得:AB2=AC2+BC2,
∴△ABC是直角三角形,
设△ABC的AB边上的高为h,
则![]() ×AB×h=
×AB×h=![]() AC×BC,即:10h=6×8,
AC×BC,即:10h=6×8,
∴h=4.8,
∴△ABC的边AB上的高为4.8.

练习册系列答案
相关题目