题目内容
如图，E、F是平行四边形ABCD的对角线AC上的点，CE=AF，请你猜想：线段BE与线段DF有怎样的关系？并对你的猜想加以说明．
平行且相等
试题分析：利用平行四边形的性质和平行线的性质可以得到相等的线段和相等的角，从而可以证明△BCE≌△DAF，进而证得结论．
∵四边形ABCD是平行四边形，
∴CB=AD，CB∥AD，
∴∠BCE=∠DAF，
∵CE=AF，
∴△BCE≌△DAF，
∴BE=DF，∠BEC=∠DFA，
∴BE∥DF，
即BE∥DF且BE=DF．
点评：解答本题的关键是熟知通常情况下，利用平行四边形的性质结合三角形全等来解决有关线段相等的证明．
练习册系列答案
相关题目
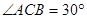，AB=4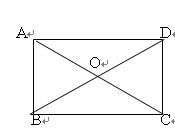
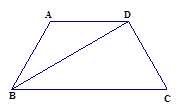
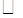ABCD的一边长为10，则对角线AC、BD的长可取下列数据中的（ ）
;
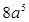，其中一条边长为
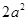，则另一条边长为 ___________。