题目内容
在矩形ABCD中,两条对角线AC、BD相交于O,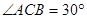 ,AB=4
,AB=4
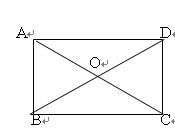
(1)判断△AOB的形状;并说明理由。
(2)求对角线AC、BD的长。
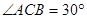 ,AB=4
,AB=4
(1)判断△AOB的形状;并说明理由。
(2)求对角线AC、BD的长。
(1)等边三角形
(2)AC=BD=8
(2)AC=BD=8
试题分析:(1)根据矩形对角线的性质可得OA=OB,易得∠BAO为60°,那么△AOB的形状为等边三角形;(2)根据(1)的结论可得OA,OB的长度,乘以2即为对角线AC、BD的长.
解:(1)△AOB为等边三角形.
∵四边形ABCD为矩形,
∴0A=OB,∠ABC=90°,
∵∠ACB=30°,
∴∠BAO=60°,
∴△AOB为等边三角形;
(2)∵△AOB为等边三角形,AB=4
∴OA=OB=AB=4,
∴AC=BD=2×4=8.
点评: 此类试题属于难度很大的试题,考生在解答此类试题时一定要掌握好矩形的性质和判定定理

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 的对角线相交于点
的对角线相交于点 ,且
,且 ,过
,过 交
交 于点
于点 ,若
,若 的周长为10,则平行四边形
的周长为10,则平行四边形
 ,∠C=45°,点P是BC边上一动点,设PB的长为x。
,∠C=45°,点P是BC边上一动点,设PB的长为x。

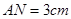 ,长
,长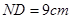 ,
,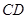 上的点
上的点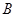 距地面的高
距地面的高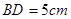 ,地面上
,地面上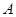 处的一只蚂蚁要到
处的一只蚂蚁要到