��Ŀ����
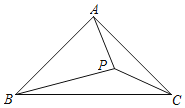
����Ŀ���������������ͼ ����������DEF����������ֱ�������ABC�ı�AB��BC��AC�ϣ������dzơ�DEF������ABC���ڽ��������Σ�
��1����֤����ADF�ա�BED��
��������������ֱ�ߺ�Բ�����������ε��ڽ���������(������ͼ�ۼ�����д����)��
��2����ͼ ��������ABC�ı߳�Ϊa��������ABC���ڽ�����DEF��ʹ��DEF�ı߳���̣���˵�����ɣ�
��3����ͼ����������ABC���ڽ�����DEF��ʹFD��AB��
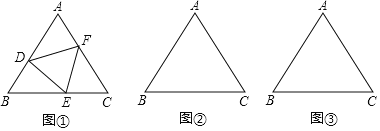
���𰸡���1��֤������������2����ͼ�����������ɼ���������3����ͼ��������
��������
���������
��1���ɵȱ������ε�����DF=DE����A=��B=60�������������ڽǺͿɵá�ADF=��BED������֤��ADF�ա�BED��
��������
��2����S��DEF=![]() ����֪��S��DEF��Сʱ��DF�ij���С����BD=x����AD=BE=a-x���ɵ�S��BED=
����֪��S��DEF��Сʱ��DF�ij���С����BD=x����AD=BE=a-x���ɵ�S��BED=![]() BEDG= =-
BEDG= =-![]() ��x-
��x-![]() ��2+
��2+![]() a2��Ȼ����ݶ��κ�����������⼴�ɣ�
a2��Ȼ����ݶ��κ�����������⼴�ɣ�
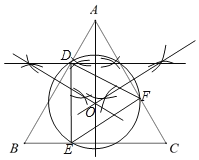
��3����AB��AC�Ĵ�ֱƽ���߽���ΪO������AO����AO�Ĵ�ֱƽ���߽�AB��D����OΪԲ�ģ�ODΪ�뾶��Բ����AC�ڵ�F����BC�ڵ�E��������⣮
֤����1���ߡ�ABC����DEF�����������Σ�
���A=��B=60������EDF=60����DF=ED��
�ߡ�ADF+��EDF=��B+��BED��
���ADF=��BED����DF=DE����A=��B=60����
���ADF�ա�BED��
��������
��2����ͼ��ʾ��
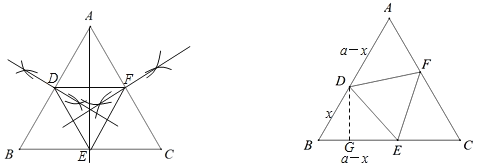
���ɣ��ɣ�1��֪��ADF�ա�BED��
ͬ����֤��BED�ա�CEF��
����ADF�ա�BED�ա�CEF��
����D��DG��BE����BD=x����AD=BE=a��x��DG=sinB��BD![]() x��
x��
S��BED![]() BEDG
BEDG![]() (a��x)��
(a��x)��![]() x
x![]() (x
(x![]() )2
)2![]() a2��
a2��
����BD![]() ������D��E��F�Ǹ����е�ʱ��S��BED�����ֵ
������D��E��F�Ǹ����е�ʱ��S��BED�����ֵ![]() a2��
a2��
��ʱ��ADF����CEF�������Ϊ���![]() a2(����ABC���ķ�֮һ)��
a2(����ABC���ķ�֮һ)��
���ڽ�����DEF�������С�����߳���̣�
��3����ͼ��ʾ��