题目内容
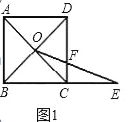
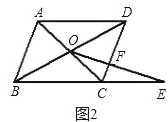
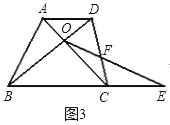
【题目】如图，在Rt△ABC中，∠ACB=90。 ， AC<BC，D为AB的中点，DE交AC于点E，DF交BC于点F，且DE⊥DF，过点A作AG／／BC交FD的延长线于点G．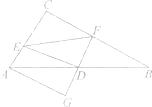
（1）求证：AG=BF；
（2）若AE=4，BF=8，求线段EF的长．
【答案】
（1）证明：∵D是AB的中点，
∴AD=BD．
∵AG∥BC，
∴∠GAD=∠FBD．
∵∠ADG=∠BDF，
∴△ADG≌△BDF．
∴AG=BF．
（2）解：连接EG，
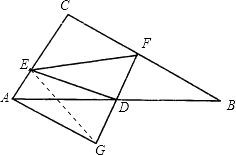
∵△ADG≌△BDF，
∴GD=FD．
∵DE⊥DF，
∴EG=EF．
∵AG∥BC，∠ACB=90°，
∴∠EAG=90°．
在Rt△EAG中，
∵EG2=AE2+AG2=AE2+BF2
∴EF2=AE2+BF2且AE=4，BF=8．
∴EF=4 
．
【解析】（1）根据中点的定义得出AD=BD ，根据平行线的性质得出∠GAD=∠FBD，根据对顶角相等得出∠ADG=∠BDF ，从而用ASA判断出△ADG≌△BDF，根据全等三角形对应边相等得出AG=BF ；
（2）连接EG，由三角形全等得出GD=FD ，根据中垂线的性质得出EG=EF ，根据二直线平行同旁内角互补得出∠EAG=90°．在Rt△EAG中，根据勾股定理及等量代换得出EF2=AE2+BF2 ，从而代指计算得出EF的长。
【考点精析】解答此题的关键在于理解线段的中点的相关知识，掌握线段的中点到两端点的距离相等，以及对平行线的性质的理解，了解两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．
练习册系列答案
相关题目
