ΧβΡΩΡΎ»ί
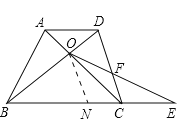
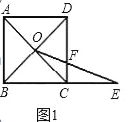
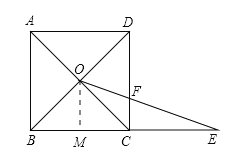
ΓΨΧβΡΩΓΩ ΐ―ßΩΈ…œΘ§’≈άœ Π≥ω ΨΝΥΈ Χβ1ΘΚ»γΆΦ1Θ§ΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§BC=1Θ§Ε‘Ϋ«œΏΫΜΒψΦ«ΉςOΘ§ΒψE «±ΏBC―”≥ΛœΏ…œ“ΜΒψΘ°Ν§Ϋ”OEΫΜCD±Ώ”ΎFΘ§…ηCE=xΘ§CF=yΘ§«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΦΑΤδΕ®“ε”ρΘ°
Θ®1Θ©Ψ≠ΙΐΥΦΩΦΘ§–ΓΟς»œΈΣΩ…“‘Ά®ΙΐΧμΦ”Η®÷ζœΏ©¹©¹ΙΐΒψOΉςOMΓΆBCΘ§¥ΙΉψΈΣM«σΫβΘ°Ρψ»œΈΣ’βΗωœκΖ®Ω…––¬πΘΩ«κ–¥≥ωΈ Χβ1ΒΡ¥πΑΗΦΑœύ”ΠΒΡΆΤΒΦΙΐ≥ΧΘΜ
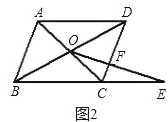
Θ®2Θ©»γΙϊΫΪΈ Χβ1÷–ΒΡΧθΦΰΓΑΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§BC=1Γ±ΗΡΈΣΓΑΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ§BC=3Θ§CD=2Θ§Γ±Τδ”ύΧθΦΰ≤Μ±δΘ®»γΆΦ2Θ©Θ§«κ÷±Ϋ”–¥≥ωΧθΦΰΗΡ±δΚσΒΡΚ· ΐΫβΈω ΫΘΜ
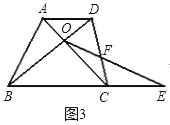
Θ®3Θ©»γΙϊΫΪΈ Χβ1÷–ΒΡΧθΦΰΓΑΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§BC=1Γ±Ϋχ“Μ≤ΫΗΡΈΣΘΚΓΑΥΡ±Ώ–ΈABCD «Χί–ΈΘ§ADΓΈBCΘ§BC=aΘ§CD=bΘ§AD=cΘ®Τδ÷–aΘ§bΘ§cΈΣ≥ΘΝΩΘ©Γ±Τδ”ύΧθΦΰ≤Μ±δΘ®»γΆΦ3Θ©Θ§«κΡψ–¥≥ωΧθΦΰ‘Ό¥ΈΗΡ±δΚσyΙΊ”ΎxΒΡΚ· ΐΫβΈω Ϋ“‘ΦΑœύ”ΠΒΡΆΤΒΦΙΐ≥ΧΘ°
ΓΨ¥πΑΗΓΩ(1) ![]() Θ°Ε®“ε”ρΈΣxΘΨ0Θ°(2)
Θ°Ε®“ε”ρΈΣxΘΨ0Θ°(2) ![]() Θ®xΘΨ0Θ©Θ°
Θ®xΘΨ0Θ©Θ°
(3) ![]() Θ®
Θ®![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷Έω: Θ®1Θ©”…ΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§Ω…ΒΟOB=ODΘ§”÷”…OMΓΆBCΘ§“Ή÷ΛΒΟOMΓΈDCΘ§”…ΤΫ––œΏΖ÷œΏΕΈ≥…±»άΐΕ®άμΦ¥Ω…«σΒΟyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©ΉςOMΓΈCDΫΜBC”ΎΒψMΘ§άϊ”ΟΘ®1Θ©÷–ΒΡΖΫΖ®Θ§Φ¥Ω…«σΒΟyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®3Θ© Ήœ»ΉςONΓΈCDΫΜBC”ΎΒψNΘ§”…ΤΫ––œΏΖ÷œΏΕΈ≥…±»άΐΕ®άμΦ¥Ω…«σΒΟyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ°
‘ΧβΫβΈω:
ΫβΘΚΘ®1Θ©»γΆΦ:
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύOB=ODΘ°
ÿOMâBCȧ
ΓύΓœOMB=ΓœDCB=90ΓψΘ§
ΓύOMΓΈDCΘ°
ΓύOM=![]() DC=
DC=![]() Θ§CM=
Θ§CM=![]() BC=
BC=![]() Θ°
Θ°
ÿOMøDCȧ
Γύ![]() Θ§
Θ§
Φ¥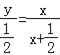 Θ§
Θ§
ΫβΒΟ![]() Θ°Ε®“ε”ρΈΣxΘΨ0Θ°
Θ°Ε®“ε”ρΈΣxΘΨ0Θ°
Θ®2Θ©![]() Θ®xΘΨ0Θ©Θ°
Θ®xΘΨ0Θ©Θ°
Θ®3Θ©»γΆΦ:
ADøBCȧ![]() ȧ
Θ§![]() Θ°
Θ°
ΙΐΒψOΉςONΓΈCDΘ§ΫΜBC”ΎΒψNΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
ÿONøCDȧ![]() ȧ
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
ΓΏONΓΈCD
Γύ![]()
Γύ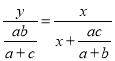
Γύ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΫβΈω ΫΈΣ
ΒΡΚ· ΐΫβΈω ΫΈΣ![]() Θ®
Θ®![]() Θ©Θ°
Θ©Θ°