题目内容
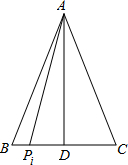
)△ABC中,AB=AC=2,BC边上有100个不同的点p1,p2,…p100;记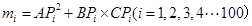 ,求
,求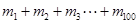 的值.
的值.
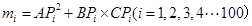 ,求
,求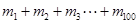 的值.
的值.400.
试题分析:作AD⊥BC于D,则BC="2BD=2CD," 根据勾股定理可得结论.
试题解析:作AD⊥BC于D,则BC=2BD=2CD.
根据勾股定理,得:APi2=AD2+DPi2=AD2+(BD-BPi)2=AD2+BD2-2BD•BPi+BPi2,
又PiB•PiC=PiB•(BC-PiB)=2BD•BPi-BPi2,
∴Mi=AD2+BD2=AB2=4,∴M1+M2+…+M10+M100=4×100=400.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 中,
中,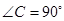 ,
,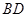 平分
平分 交AC于点D,若CD=6,则点D到AB的距离为 .
交AC于点D,若CD=6,则点D到AB的距离为 .