题目内容
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合).
重合).![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.

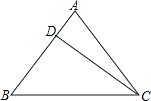
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
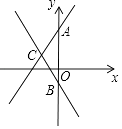
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析(2)成立,理由见解析;(3)①30°.②1+![]() .
.
【解析】
试题分析:(1)只要证明AE=BM,AE∥BM即可解决问题;
(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;
AM,MI⊥AC,即可解决问题;
②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得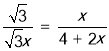 ,解方程即可;
,解方程即可;
试题解析:(1)证明:如图1中,
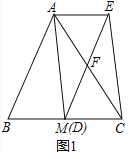
∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.

∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(3)①如图3中,取线段HC的中点I,连接MI,
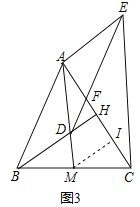
∵BM=MC,
∴MI是△BHC的中位线,
∴∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM.
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,
∴BH=4+2x,
∵四边形ABDE是平行四边形,
∴DF∥AB,
∴![]() ,
,
∴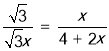 ,
,
解得x=1+![]() 或1-
或1-![]() (舍弃),
(舍弃),
∴DH=1+![]() .
.