题目内容
【题目】如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.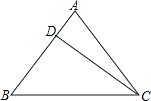
【答案】解:在△BCD中,BC=20cm,CD=16cm,BD=12cm,
∵BD2+DC2=BC2,
∴△BCD中是直角三角形,∠BDC=90°,
设AD=x,则AC=x+12,
在Rt△ADC中,∵AC2=AD2+DC2,
∴x2+162=(x+12)2,
解得: ![]() .
.
∴△ABC的周长为:( ![]() +12)×2+20=
+12)×2+20= ![]() cm.
cm.
【解析】根据勾股定理的逆定理BD2+DC2=BC2,得到△BCD中是直角三角形,∠BDC=90°,根据勾股定理得到在Rt△ADC中,∵AC2=AD2+DC2,求出△ABC的周长.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.

练习册系列答案
相关题目