Question

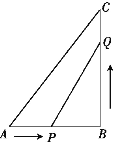
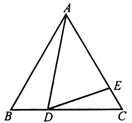
【题目】如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADB＋∠EDC＝120°．

（1）求证：△ABD∽△DCE；

（2）若BD＝4，CE＝3，求△ABC的面积．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）根据等边三角形性质求出∠B=∠C=60°，由∠ADB＋∠EDC＝120°，根据等式性质求出∠BAD=∠CDE，即可证明△ABD∽△DCE；

（2）由（1）知道△ABD∽△DCE，对应边成比例得出，列方程解答即可．

（1）证明：∵△ABC是等边三角形，

∴∠B=∠C=60°，AB=AC，

∴∠BAD+∠ADB=120°，

又∵∠ADB+∠EDC=120°，

∴∠BAD=∠EDC，

∴△ABD∽△DCE.

（2）由（1）△ABD∽△DCE可得：，

∴，

∴4(AB-4)=3AB，

∴AB=16.

过点A作AF⊥BC于F，则BF=BC=8，

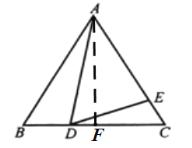
在Rt△ABF中，AF==，

∴△ABC的面积为：.