题目内容
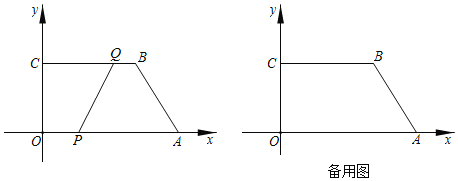
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边向OA终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ![]() =y.
=y.
(1)直接写出y关于t的函数解析式及t的取值范围: ;
(2)当PQ=3![]() 时,求t的值;
时,求t的值;
(3)连接OB交PQ于点D,若双曲线![]() 经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,由点
,由点![]() ,
,![]() 的出发点、速度及方向可找出当运动时间为
的出发点、速度及方向可找出当运动时间为![]() 秒时点
秒时点![]() ,
,![]() 的坐标,进而可得出
的坐标,进而可得出![]() ,
,![]() 的长,再利用勾股定理即可求出
的长,再利用勾股定理即可求出![]() 关于
关于![]() 的函数解析式(由时间
的函数解析式(由时间![]() 路程
路程![]() 速度可得出
速度可得出![]() 的取值范围);
的取值范围);
(2)将![]() 代入(1)的结论中可得出关于
代入(1)的结论中可得出关于![]() 的一元二次方程,解之即可得出结论;
的一元二次方程,解之即可得出结论;
(3)连接![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,利用勾股定理可求出
,利用勾股定理可求出![]() 的长,由
的长,由![]() 可得出
可得出![]() ,利用相似三角形的性质结合可
,利用相似三角形的性质结合可![]() 求出
求出![]() ,由
,由![]() 可得出
可得出![]() ,在
,在![]() 中可求出
中可求出![]() 及
及![]() 的值,由
的值,由![]() ,
,![]() 可求出点
可求出点![]() 的坐标,再利用反比例函数图象上点的坐标特征即可求出
的坐标,再利用反比例函数图象上点的坐标特征即可求出![]() 值,此题得解.
值,此题得解.
解:(1)过点![]() 作
作![]() 于点
于点![]() ,如图1所示.
,如图1所示.

当运动时间为![]() 秒时时
秒时时![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,|
,|![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() .
.
(2)当![]() 时,
时,![]() ,
,
整理,得:![]() ,
,
解得:![]() .
.
(3)经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值不变.
值不变.
连接![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
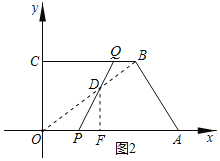
于点![]() ,如图2所示.
,如图2所示.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 经过点
经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值为
值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误