题目内容
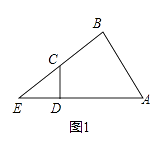
【题目】已知一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,![]() ,
,![]()
![]() 图1中
图1中![]() ______
______![]()
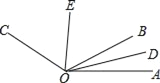
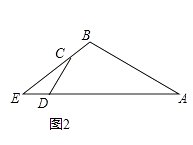
![]() 如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度
如图2,三角板COD固定不动,将三角板AOB绕着点O按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线EF的上方:
,在转动过程中两块三角板都在直线EF的上方:
![]() 当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度
当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
![]() 是否存在
是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)75(2)①![]() ,
,![]() ,
,![]() ②当
②当![]() 或
或![]() 时,存在
时,存在![]()
【解析】
(1)根据平平角的定义即可得到结论;
(2)①根据已知条件和角平分线的定义即可得到结论;
②当OA在OD的左侧时,当OA在OD的右侧时,列方程即可得到结论.
解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°∠AOB∠COD=75°,
故答案为:75;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°∠AOE∠COD=120°α,
∴∠AOB=![]() ∠AOD=60°
∠AOD=60°![]() α=45°,
α=45°,
∴α=30°,
当OB平分∠AOC时,
∵∠AOC=180°α,
∴∠AOB═90°![]() α=45°,
α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°45°30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°α,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(120°α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α120°,∠BOC=135°α,
∵∠BOC=2∠AOD,
∴135°α=2(α120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目