��Ŀ����
����Ŀ����֪�ı���ABCD��һ��Ա�AD��BC���ӳ��߽��ڵ�E��
��1����ͼ1������ABC=��ADC=90�㣬��֤��EDEA=ECEB��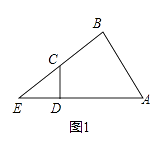
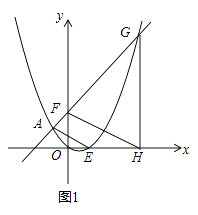
��2����ͼ2������ABC=120�㣬cos��ADC= ![]() ��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������
��CD=5��AB=12����CDE�����Ϊ6�����ı���ABCD�������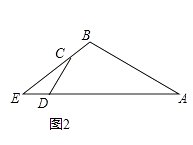
��3����ͼ3����һ��Ա�AB��DC���ӳ����ཻ�ڵ�F����cos��ABC=cos��ADC= ![]() ��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
��CD=5��CF=ED=n��ֱ��д��AD�ij����ú�n��ʽ�ӱ�ʾ��
���𰸡�
��1���⣺��ͼ1�У�
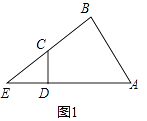
�ߡ�ADC=90�㣬��EDC+��ADC=180�㣬
���EDC=90�㣬
�ߡ�ABC=90�㣬
���EDC=��ABC��
�ߡ�E=��E��
���EDC�ס�EBA��
�� ![]() =
= ![]() ��
��
��EDEA=ECEB��
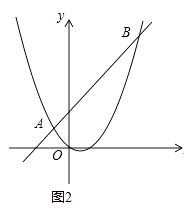
��2���⣺��ͼ2�У���C��CF��AD��F��AG��EB��G��
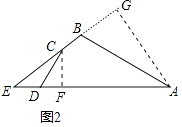
��Rt��CDF��cos��ADC= ![]() ��
��
�� ![]() =
= ![]() ����CD=5��
����CD=5��
��DF=3��
��CF= ![]() =4��
=4��
��S��CDE=6��
�� ![]() EDCF=6��
EDCF=6��
��ED= ![]() =3��EF=ED+DF=6��
=3��EF=ED+DF=6��
�ߡ�ABC=120�㣬��G=90�㣬��G+��BAG=��ABC��
���BAG=30�㣬
����Rt��ABG��BG= ![]() AB=6��AG=
AB=6��AG= ![]() =6
=6 ![]() ��
��
��CF��AD��AG��EB��
���EFC=��G=90�㣬�ߡ�E=��E��
���EFC�ס�EGA��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EG=9 ![]() ��
��
��BE=EG��BG=9 ![]() ��6��
��6��
��S�ı���ABCD=S��ABE��S��CDE= ![]() ��9
��9 ![]() ��6����6
��6����6 ![]() ��6=75��18
��6=75��18 ![]() ��
��
��3���⣺��ͼ3�У���CH��AD��H����CH=4��DH=3��

��tan��E= ![]() ��
��
��AG��DF�ڵ�G����AD=5a����DG=3a��AG=4a��
��FG=DF��DG=5+n��3a��
��CH��AD��AG��DF����E=��F��
��֤��AFG�ס�CEH��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��a= ![]() ��
��
��AD=5a= ![]() ��
��
��������Ҫ֤�˻�ʽ��ʽ�������ɻ�Ϊ����ʽ��![]() ��������һ��ȷ�������Ρ�EDC���EBA���ƣ���2������ǡ����Ǻ���Ӧ����ֱ�������������ã�����������߹���ֱ�������Σ�ǡ�ù�����ڣ�1�����ͼ�Σ������һ�ʵ�˼·�����EG����һ���������֮�����ı���ABCD�����.��3�������߹����ֱ�������Σ��������������Ρ�AFG�ס�CEH����������ʽ�����AD�ij�.
��������һ��ȷ�������Ρ�EDC���EBA���ƣ���2������ǡ����Ǻ���Ӧ����ֱ�������������ã�����������߹���ֱ�������Σ�ǡ�ù�����ڣ�1�����ͼ�Σ������һ�ʵ�˼·�����EG����һ���������֮�����ı���ABCD�����.��3�������߹����ֱ�������Σ��������������Ρ�AFG�ס�CEH����������ʽ�����AD�ij�.
�����㾫�����������⣬������Ҫ�˽����������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)����Ҫ����������Ǻ����Ķ���(���A�����ҡ����ҡ����С����ж�������A��������Ǻ���)�����֪ʶ���Ǵ���Ĺؼ���

����Ŀ���ܺ���Ӱ�죬�Ա����ϵĵ���ȡů�����ۻ�����ij��������ÿ̨�ɱ��۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȡů�����±��ǽ���������������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȡů�������۵��ۣ�
��2�����������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȡů����30̨����A���ͺŵĵ���ȡů������ܲɹ�����̨��