题目内容
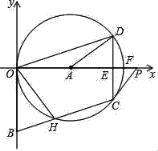
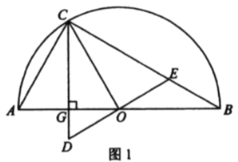
【题目】如图，△ABC中，∠B＝45°，BC＝4，BC边上的高AD＝1，点P1、Q1、H1分别在边AD、AC、CD上，且四边形P1Q1H1D为正方形，点P2、Q2、H2分别在边Q1H1、CQ1、CH1上，且四边形P2Q2H2H1为正方形，…，按此规律操作下去，则线段CQ2020的长度为________
【答案】
【解析】
先求得BD、DC、AC的长，设P1D=x，则AP1=-x，P1Q1=H1Q1=H1D=P1D=x，再根据正方形性质可得AD//Q1H1,所以△ADC∽△CH1Q1,然后求的△ADC和△CH1Q1的相似比，同理求得△Q1H1C和△CH2Q2的相似比，然后总结规律即可解答．
解：∵BC边上的高AD＝1，∠B＝45°
∴BD=1
∴DC=BC-BD=4-1=3
∵AD⊥DC
∴AC=
设P1D=x，则AP1=-x，P1Q1=H1Q1=H1D=P1D =x
∵P1Q1H1D是正方形
∴AD//Q1H1，
∴△ADC∽△CH1Q1,
∴
即
，解得x=
∴P1Q1=H1Q1=H1D=P1D=，
∴△ADC和△CH1Q1的相似比为
同理：△Q1H1C和△CH2Q2的相似比
∴△ADC和△CH2Q2的相似比
依次类推，△ADC和△CH2020Q2020的相似比为
∴
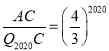即
∴
=
故答案为．
阅读快车系列答案【题目】随着“微信运动”被越来越多的人关注和喜爱，某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数 | 频数 | 频率 |
0≤x＜4000 | 8 | 0.16 |
4000≤x＜8000 | 15 | 0.3 |
8000≤x＜12000 | 12 | a |
12000≤x＜16000 | b | 0.2 |
16000≤x＜20000 | 3 | 0.06 |
20000≤x＜24000 | 2 | 0.04 |
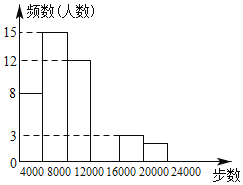
请根据以上信息，解答下列问题：
（1）写出a，b的值并补全频数分布直方图；
（2）我市约有5000名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？
（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，用树形图或列表法求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．
