题目内容
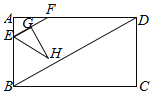
【题目】如图1,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 在半圆上,连结
在半圆上,连结![]() 且
且![]() .连结
.连结![]() 是
是![]() 边上的高,过点
边上的高,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]()
![]() 当
当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值.
的值.
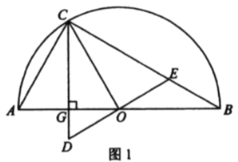
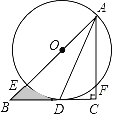
![]() 如图2,取
如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() .若
.若![]() 在点
在点![]() 运动过程中,当四边形
运动过程中,当四边形![]() 的其中一边长是
的其中一边长是![]() 的
的![]() 倍时,求所有满足条件的
倍时,求所有满足条件的![]() 长.
长.

【答案】(1)证明见解析;(2)![]() ;(3) OG的长为
;(3) OG的长为![]() 或
或![]()
【解析】
(1)根据圆周角定理得到![]() ,再利用等边对等角以及等角的余角相等即可证明;
,再利用等边对等角以及等角的余角相等即可证明;
(2)根据中垂线的判定和性质以及等角的余角相等可求得![]() ,利用特殊角的三角函数值即可求解;
,利用特殊角的三角函数值即可求解;
(3) 分![]() ,
,![]() ,
,![]() 三种情况讨论,设参数,利用勾股定理构建方程即可求解.
三种情况讨论,设参数,利用勾股定理构建方程即可求解.
(1)证明:
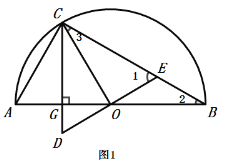
![]() 为
为![]() 直径,
直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
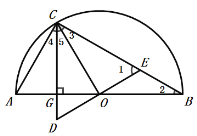
(2)![]() ,
,![]() 为
为![]() 中点,
中点,
![]() 为
为![]() 中垂线,
中垂线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 为
为![]() 中点,
中点,
![]() ,
,![]() ,
,
四边形![]() ,除
,除![]() 外还有三边,
外还有三边,
故分![]() 类讨论:设
类讨论:设![]() ,
,
①当![]() 时,则
时,则![]() ,
,
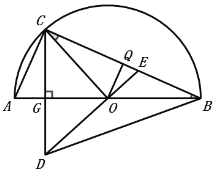
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
整理得![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() ;
;
②当![]() 时,则
时,则![]() ,
,
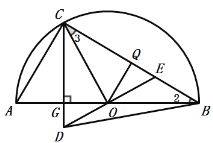
在![]() 中,
中,![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
即![]() ,
,
![]() ,
,
∵![]()
![]() ,
,
即 ,
,
![]() ,
,
∴![]() ;
;
③当![]() 时,则
时,则![]() ,
,
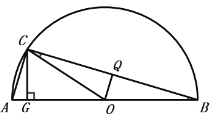
由①得:![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
联立: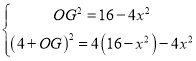 ,
,
解得:![]() ,
,
∴![]() ,四边形
,四边形![]() 不存在;
不存在;
综上,OG的长为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目