题目内容
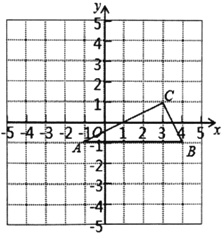
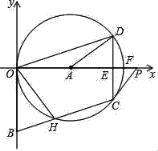
【题目】如图,⊙A过OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).
(1)若∠BOH=30°,求点H的坐标;
(2)求证:直线PC是⊙A的切线;
(3)若OD=![]() ,求⊙A的半径.
,求⊙A的半径.
【答案】(1)(1,﹣![]() );(2)详见解析;(3)
);(2)详见解析;(3)![]() .
.
【解析】
(1)先判断出OH=OB=2,利用三角函数求出MH,OM,即可得出结论;
(2)先判断出∠PCD=∠DAE,进而判断出∠PCD=∠CAE,即可得出结论;
(3)先求出OE═3,进而用勾股定理建立方程,r2-(3-r)2=1,即可得出结论.
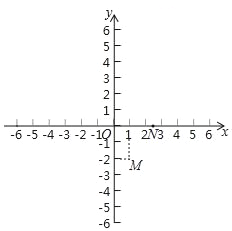
(1)解:如图,过点H作HM⊥y轴,垂足为M.
∵四边形OBCD是平行四边形,
∴∠B=∠ODC
∵四边形OHCD是圆内接四边形
∴∠OHB=∠ODC
∴∠OHB=∠B
∴OH=OB=2
∴在Rt△OMH中,
∵∠BOH=30°,
∴MH=![]() OH=1,OM=
OH=1,OM=![]() MH=
MH=![]() ,
,
∴点H的坐标为(1,﹣![]() ),
),
(2)连接AC.
∵OA=AD,
∴∠DOF=∠ADO
∴∠DAE=2∠DOF
∵∠PCD=2∠DOF,
∴∠PCD=∠DAE
∵OB与⊙O相切于点A
∴OB⊥OF
∵OB∥CD
∴CD⊥AF
∴∠DAE=∠CAE
∴∠PCD=∠CAE
∴∠PCA=∠PCD+∠ACE=∠CAE+∠ACE=90°
∴直线PC是⊙A的切线;
(3)解:⊙O的半径为r.
在Rt△OED中,DE=![]() CD=
CD=![]() OB=1,OD=
OB=1,OD=![]() ,
,
∴OE═3
∵OA=AD=r,AE=3﹣r.
在Rt△DEA中,根据勾股定理得,r2﹣(3﹣r)2=1
解得r=![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
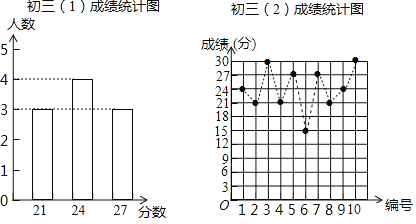
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 |
初三(1)班 | __________ | 24 | ________ |
初三(2)班 | 24 | _________ | 21 |
(2)若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察上图的数据分布情况,请通过计算说明哪个班的学生纠错的得分更稳定.