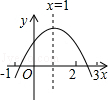题目内容
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则下列图象中,能表示y与x的函数关系的图象大致是( )




D.
试题分析:过点P作PF⊥BC于F,若要求△PBE的面积,则需要求出BE,PF的值,利用已知条件和正方形的性质以及勾股定理可求出BE,PF的值.再利用三角形的面积公式得到y与x的关系式,此时还要考虑到自变量x的取值范围和y的取值范围.
过点P作PF⊥BC于F,

∵PE=PB,
∴BF=EF,
∵正方形ABCD的边长是1,
∴AC=
 ,
,∵AP=x,∴PC=
 -x,
-x,∴PF=FC=
 (
( -x)=1-
-x)=1- ,
,∴BF=FE=1-FC=
 x,
x,∴S△PBE=
 BE•PF=
BE•PF= x(1-
x(1- )=-
)=- x2+
x2+ ,
,即y=-
 x2+
x2+ ,(0<x<
,(0<x< ),
),∴y是x的二次函数(0<x<
 ),
),故选D.
考点: 动点问题的函数图象.

练习册系列答案
相关题目
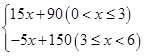 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=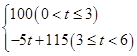
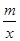 的交点A的横坐标是2,则关于x的不等式
的交点A的横坐标是2,则关于x的不等式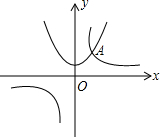
 x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A,以O为圆心,OA为半径作圆,在第四象限内与抛物线y=
x2通过平移得到抛物线m,抛物线m经过点B(6,0)和O(0,0),它的顶点为A,以O为圆心,OA为半径作圆,在第四象限内与抛物线y=
 的图象经过点
的图象经过点 ,对称轴为直线
,对称轴为直线 ,下列5个结论:①
,下列5个结论:① ; ②
; ② ; ③
; ③ ;④
;④ ; ⑤
; ⑤ ,
,
 的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是( )
的顶点是点P,对称轴与x轴相交于点Q,以点P为圆心,PQ长为半径画⊙P,那么下列判断正确的是( )