��Ŀ����
����Ŀ����ͼ����Rt��ABC�У���ACB��90����AC��BC��4cm����P�ӵ�A������lcm/s���ٶ�������AC��CB�˶�������P��PQ��AB�ڵ�Q������P�����A��B�غ�ʱ�����߶�PQΪ��������������PQRS����������PQRS����ABC���ص��������ΪS����P���˶�ʱ��Ϊt��s����
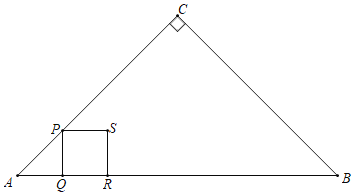
��1���ú�t�Ĵ���ʽ��ʾCP�ij��ȣ�
��2������S����BC����ʱ����t��ֵ��
��3����������PQRS����ABC���ص����ֲ��������ʱ����S��t֮��ĺ�����ϵʽ��
��4������CS����ֱ��CS����ABC�����ֵ������Ϊ1��2ʱ��ֱ��д��t��ֵ��
���𰸡���1����0��t��4ʱ��CP��4��t����4��t��8ʱ��CP��t��4����2��![]() ����3��S��
����3��S��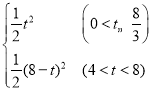 ����4��
����4��![]() ��
��![]()
��������
��1�����������ηֱ���⼴�ɣ�
��2������PA+PC��4���������̼��ɽ�����⣮
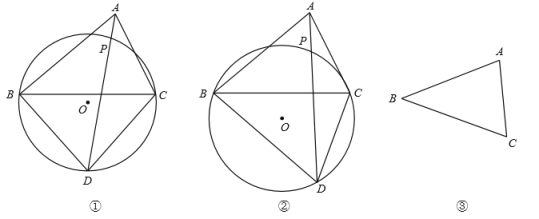
��3�����������Σ���ͼ2�У���0��t��![]() ʱ���ص�������������PQRS����4��t��8ʱ���ص������ǡ�PQB���ֱ���⼴�ɣ�
ʱ���ص�������������PQRS����4��t��8ʱ���ص������ǡ�PQB���ֱ���⼴�ɣ�
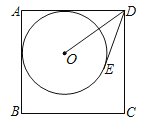
��4����ֱ��CS��AB��E�����������Σ���ͼ4��1�У���AE��![]() AB��
AB��![]() ʱ��������������ͼ4��2�У���AE��
ʱ��������������ͼ4��2�У���AE��![]() ABʱ�������������ֱ���⼴�ɽ�����⣮
ABʱ�������������ֱ���⼴�ɽ�����⣮
�⣺��1����0��t��4ʱ����AC��4��AP��t��
��PC��AC��AP��4��t��
��4��t��8ʱ��CP��t��4��
��2����ͼ1�У���S����BC���ϣ�
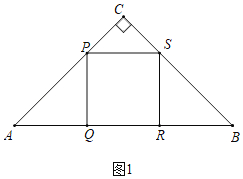
��PA��t��AQ��QP����AQP��90����
��AQ��PQ��PS��![]() t��
t��
��CP��CS����C��90����
��PC��CS��![]() t��
t��
��AP+PC��BC��4��
��t+![]() t��4��
t��4��
���t��![]() ��
��
��3����ͼ2�У���0��t��![]() ʱ���ص�������������PQRS��S����
ʱ���ص�������������PQRS��S����![]() t��2��
t��2��![]() t2��
t2��
��4��t��8ʱ���ص������ǡ�PQB��S��![]() ��8��t��2��
��8��t��2��

����������S��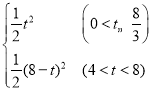 ��
��
��4����ֱ��CS��AB��E��
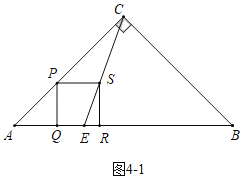
��ͼ4��1�У���AE��![]() AB��
AB��![]() ʱ������������
ʱ������������
��PS��AE��
��![]() ��
��
��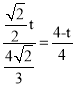 ��
��
���t��![]() ��
��
��ͼ4��2�У���AE��![]() ABʱ������������
ABʱ������������
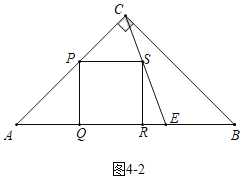
ͬ���ɵã�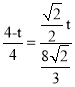 ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��
��![]() ��
��