Question

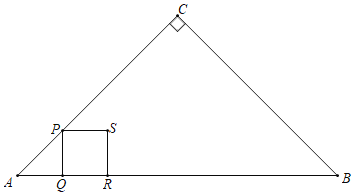
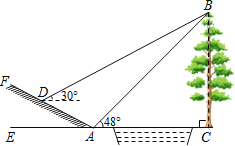
【题目】如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i＝1：，求大树的高度．（结果保留一位小数）参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，取1.73．

Answer 1

【答案】树高BC约12.5米．

【解析】

首先过点D作DM⊥BC于点M，DN⊥AC于点N，由FA的坡比i=1：

，DA=6，可求得AN与DN的长，然后设大树的高度为x，又由在斜坡上A处测得大树顶端B的仰角是48°，可得AC=，又由在△BDM中，，可得x﹣3＝（3+），继而求得答案．

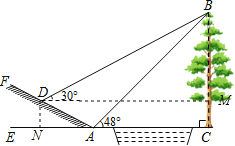
过点D作DM⊥BC于点M，DN⊥AC于点N，

则四边形DMCN是矩形，

∵DA＝6，斜坡FA的坡比i＝1：，

∴DN＝AD＝3，AN＝ADcos30°＝6×＝3，

设大树的高度为x，

∵在斜坡上A处测得大树顶端B的仰角是48°，

∴tan48°＝≈1.11，

∴AC＝，

∴DM＝CN＝AN+AC＝3+，

∵在△BDM中，，

BM＝DM，

∴x﹣3＝（3+），

解得：x≈12.5．

答：树高BC约12.5米．