题目内容
【题目】在四边形ABCD中,AB=AD,BC=CD.
(1)如图1,请连接AC,BD,求证:AC垂直平分BD;
(2)如图2,若∠BCD=60°,∠ABC=90°,E,F分别为边BC,CD上的动点,且∠EAF=60°,AE,AF分别与BD交于G,H,求证:△AGH∽△AFE;
(3)如图3,在(2)的条件下,若 EF⊥CD,直接写出![]() 的值.
的值.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题(1)由题意分别求出A,C点在BD垂直平分线上,所以AC就是BD的垂直平分线.(2) ,将△ABE绕点A逆时针旋转120得到△ADM.连接AC交BD于O.先证明F、D、M共线,再通过倒角得到∠GAH=∠FAE,所以△AGH∽△AFE.
(3)连接AC交BD于O,作HM⊥AD于M, 设HM=AM=a,则DH=2a,DM=![]() a,
a,
用a表示GH,BD,求出比值.
试题解析:
(1)证明:如图1中,连接BD、AC.
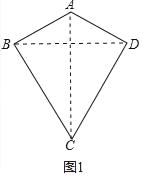
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴AC是线段BD的垂直平分线,
即AC垂直平分线段BD.
(2)如图2中,将△ABE绕点A逆时针旋转120°得到△ADM.连接AC交BD于O.
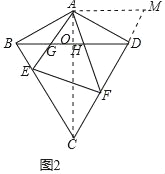
∵B、D关于AC对称,
∴∠ABC=∠ADC=90°,
∵∠BCD=60°,
∴∠BAD=120°,
∵∠EAF=60°,
∴∠BAE+∠DAF=∠DAF+∠DAM=60°,
∴∠FAE=∠FAM,
∵∠ADM=∠ABE=90°=∠ADF,
∴F、D、M共线,
∵FA=FA,AE=AM,
∴△FAE≌△FAM,
∴∠AFE=∠AFM,
∵∠CAD=∠CAB=60°=∠EAF,
∴∠GAO=∠DAF,
∵∠AGO+∠GAO=90°,∠AFD+∠FAD=90°,
∴∠AGO=∠ADF,
∴∠AGH=∠AFE,∵∠GAH=∠FAE,
∴△AGH∽△AFE.
(3)解:如图3中,连接AC交BD于O,作HM⊥AD于M.
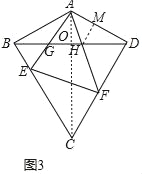
∵EF⊥CD,
∴∠EFD=90°,
由(2)可知∠AFD=∠AFE=∠AGO=45°,
∵∠ADF=90°,
∴AD=DF,设HM=AM=a,则DH=2a,DM=![]() a,
a,
在Rt△ACD中,∵∠ACD=30°,AD=(1+![]() )a,
)a,
∴CD=BD=![]() AD=(3+
AD=(3+![]() )a,
)a,
在Rt△AHD中,∵∠ADH=30°,AD=(1+![]() )a,
)a,
∴AO=OG=![]() AD=
AD=![]() a,OD=
a,OD=![]() OA=
OA=![]() a,
a,
∴OH=OD﹣DH=![]() a,﹣2a=
a,﹣2a=![]() a,
a,
∴GH=OG+OH=![]() a,
a,
∴![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
【题目】为增强公民的节约意识,合理利用天然气资源,某市自![]() 月
月![]() 日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元 |
不超出 |
|
超出 |
|
超出 |
|
(1)若某用户![]() 月份用气量为
月份用气量为![]() ,交费多少元?
,交费多少元?
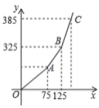
(2)调价后每月支付燃气费用![]() (单位:元)与每月用气量
(单位:元)与每月用气量![]() (单位:
(单位:![]() )的关系如图所示,求
)的关系如图所示,求![]() 与
与![]() 的解析式及
的解析式及![]() 的值.
的值.