Question

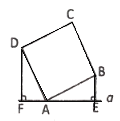
【题目】如图，直线过正方形的顶点，点、到直线的距离分别为、，则正方形的周长为_________.

Answer 1

【答案】

【解析】

根据正方形性质得出AD=AB，∠BAD=90°，求出∠EAB=∠FDA，证△AEB≌△DFA，求出DF=AE=4，在Rt△AED中，由勾股定理求出AD，即可求出正方形的面积．

解：∵四边形ABCD是正方形，
∴AD=AB，∠BAD=90°，
∵BE⊥EF，DF⊥EF，
∴∠AEB=∠DFA=90°，
∴∠FAD+∠BAE=180°-90°=90°，∠ABE+∠EAB=90°，
∴∠FAD=∠EBA，
∵在△AEB和△DAF中

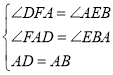
∴△AEB≌△DAF（AAS），
∴DF=AE=4，
在Rt△AFD中，由勾股定理得：AD=

即正方形ABCD的面积是5×4=20.

故答案为：20.