��Ŀ����
��ͼ��ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A��B������ֱ�Ϊ��4��0������4��3��������M��N�ֱ��O��Bͬʱ��������ÿ��1����λ���ٶ��˶������У���M��OA���յ�A�˶�����N��BC���յ�C�˶�������M��MP��OA��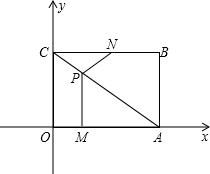 ��AC��P������NP����֪�����˶���x�룮
��AC��P������NP����֪�����˶���x�룮��1��P�������Ϊ��
��2�������NPC���S�ı���ʽ����������S�����ֵ����Ӧ��xֵ��
��3�����ı���OMPC�����ΪS1���ı���ABNP�����ΪS2�������x��ȡֵ��Χ����S1��S2�Ĵ�С��ϵ��˵�����ɣ�
��4����xΪ��ֵʱ����NPC��һ�����������Σ�
��������1�����ȸ�������õ�C��M��N���������ֵ�����������������Ǻ����Ĺ�ϵ�������õ�P�������ֵ��
��2�����NPC�����ΪS���ڡ�NPC�����ݣ�1����֪CN�ij�����x�ı���ʽ��NC���ϵĸ߹���x�ı���ʽ������������������ļ��㹫ʽ��ã�S����x���κ�������ʽ����x��ȡֵ��Χ����ö��κ��������ֵ��
��3���������ε�������㹫ʽд��S1����x�ı���ʽ������S2=S��ABC-S��PCNд������x�Ĺ�ϵʽ���پ�0��x��4��ȡֵ������S1��S2�Ĵ�С��ϵ��
��4�������ӳ�MP��CB��Q������PQ��BC���ٷֽ�͢���NP=CP������CP=CN������CN=NP�����������x��ȡֵ��
��2�����NPC�����ΪS���ڡ�NPC�����ݣ�1����֪CN�ij�����x�ı���ʽ��NC���ϵĸ߹���x�ı���ʽ������������������ļ��㹫ʽ��ã�S����x���κ�������ʽ����x��ȡֵ��Χ����ö��κ��������ֵ��
��3���������ε�������㹫ʽд��S1����x�ı���ʽ������S2=S��ABC-S��PCNд������x�Ĺ�ϵʽ���پ�0��x��4��ȡֵ������S1��S2�Ĵ�С��ϵ��
��4�������ӳ�MP��CB��Q������PQ��BC���ٷֽ�͢���NP=CP������CP=CN������CN=NP�����������x��ȡֵ��
����⣺��1���������֪��C��0��3����M��x��0����N��4-x��3����
���P����Ϊ(x��3-
x)��2�֣�
��2�����NPC�����ΪS��
�ڡ�NPC�У�NC=4-x��NC���ϵĸ�Ϊ
x������0��x��4��
��S=
��4-x����
x=-
��x-2��2+
��
��S�����ֵΪ
����ʱx=2��3�֣�
��3����ͼ��֪��S1=
(OC+MP)•OM=
(3+3-
x)•x
S2=S��ABC-S��PCN=
•4•3-
(4-x)��
x��
��0��x��2ʱ��S1��S2����x=2ʱ��S1=S2����2��x��4ʱ��S1��S2����3�֣�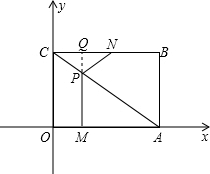
��4���ӳ�MP��CB��Q������PQ��BC��
����NP=CP����PQ��BC����NQ=CQ=x����3x=4����x=
��
����CP=CN����CN=4-x��PQ=
x��CP=
x��4-x=
x��x=
��
����CN=NP����CN=4-x����PQ=
x��NQ=4-2x����Rt��PNQ��PN2=NQ2+PQ2
�ࣨ4-x��2=��4-2x��2+��
x��2����x=
��
����������x=
����x=
����x=
����3�֣�
���P����Ϊ(x��3-
| 3 |
| 4 |
��2�����NPC�����ΪS��
�ڡ�NPC�У�NC=4-x��NC���ϵĸ�Ϊ
| 3 |
| 4 |
��S=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
��S�����ֵΪ
| 3 |
| 2 |
��3����ͼ��֪��S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
S2=S��ABC-S��PCN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
��0��x��2ʱ��S1��S2����x=2ʱ��S1=S2����2��x��4ʱ��S1��S2����3�֣�

��4���ӳ�MP��CB��Q������PQ��BC��
����NP=CP����PQ��BC����NQ=CQ=x����3x=4����x=
| 4 |
| 3 |
����CP=CN����CN=4-x��PQ=
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 16 |
| 9 |
����CN=NP����CN=4-x����PQ=
| 3 |
| 4 |
�ࣨ4-x��2=��4-2x��2+��
| 3 |
| 4 |
| 128 |
| 57 |
����������x=
| 4 |
| 3 |
| 16 |
| 9 |
| 128 |
| 57 |
���������⿼���˶��κ�����������������������������Ҫ֪ʶ�㣬�õ��˷������۵���ѧ˼�룬�ѵ����ڿ�������Ҫȫ�棬�������ز�©��

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫����
��ͼ��ƽ��ֱ������ϵ�У�OΪֱ��������ABC��ֱ�Ƕ��㣬��B=30�㣬��Ƕ���A��˫���� =2
=2 ��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
��ͼ��ƽ��ֱ������ϵ�У�OB��x���ϣ���ABO=90�㣬��A������Ϊ��1��2��������AOB�Ƶ�A��ʱ����ת90�㣬���O�Ķ�Ӧ��C������Ϊ��������
 ��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
��ͼ��ƽ��ֱ������ϵ�У�A������Ϊ��8��0����B������Ϊ��0��6��C���߶�AB���е㣮������y�����Ƿ����һ��P��ʹ����P��B��CΪ��������������AOB���ƣ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�