Question

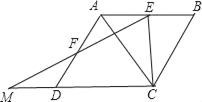
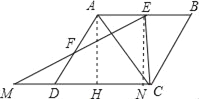
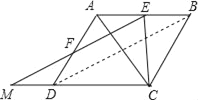
【题目】已知，如图，四边形ABCD是边长为2的菱形，E、F分别是AB、AD的中点，连EF，将△FAE绕点F旋转180°得△FDM．

（1）求证：EF⊥AC．

（2）若∠B=60°，求以E、M、C为顶点的三角形的面积．

Answer 1

【答案】（1）证明见解析；（2）S△MEC=．

【解析】试题分析：(1)连BD,由四边形ABCD是菱形,可得AC⊥BD,又由E、F分别是AB、AD的中点,根据三角形中位线的性质,即可证得EF⊥AC;

(2)由旋转的性质,即可得△FDM≌△FAE,又由菱形的性质,可证得∠MDF+∠FDC=180 ,即M、D、C三点共线,然后作AH⊥DC于H,作EN⊥DC于N,利用三角函数的知识即可求得EN的值,则可求得以E、M、C为顶点的三角形的面积.

解：（1）证明：连BD，

∵四边形ABCD是菱形，

∴AC⊥BD．

又∵E、F分别为AB、AD的中点，

∴EF∥BD，

∴AC⊥EF．

（2）依题意，△FAE绕F点旋转180°得△FDM，

∴△FDM≌△FAE，

∴∠EAF=∠MDF．

又∵菱形ABCD中，AB∥DC，∠EAF+∠FDC=180°，

∴∠MDF+∠FDC=180°，

∴M、D、C三点共线，

作AH⊥DC于H，作EN⊥DC于N，

则EN=AH．

∵AD=2，∠ADC=∠B=60°，

∴AH=ADsin60°==EN．

又∵MD=EA=AB=1，DC=2，

∴MC=MD+CD=3，

∴S△MEC=MCEN=×3×=．