��Ŀ����
����Ŀ����֪����ʽ��a2��16��x2+��a+4��x+4a�ǹ���x��һ�ζ���ʽ���ҳ�����Ϊb��a��b�ֱ��Ӧ�������ϵ�A��B���㣮
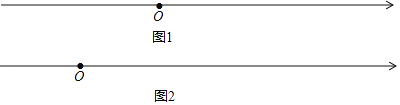
��1��a���� ����b���� ����
��2������P�ӵ�A��������ÿ��3����λ���ȵ��ٶ���x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�ľ����3����
��3�������ϻ���һ��C��ʾ����Ϊ40������P�͵�Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��4����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ���C���˶���P�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����˶�������ʱ��P��Q����֮��ľ���Ϊ6��
���𰸡���1��4��16����2����ʱ��Ϊ3���6��ʱ����P����A�ľ����ǵ�P����B�ľ����3������3�����˶�3�롢9�롢11���27��ʱ��P��Q����֮��ľ���Ϊ6��
��������
��1��������a2��16��x2+��a+4��x+4a�ǹ���x��һ�ζ���ʽ����֪��a2��16��0��a+4��0���������a��ֵ��������������b��ֵ��
��2���������⣬�ú���t�Ĵ���ʽ��ʾ��P����Ӧ�������������ۣ��г�����t��һԪһ���̣�������⣻
��3���������⣬�ֱ��ú���t����ʽ��ʾP��Q����Ӧ��������A��B��C��P��Q�����λ�ã����з������ۣ��г�����t��һԪһ�η��̣��������.
��1���ߣ�a2��16��x2+��a+4��x+4a�ǹ���x��һ�ζ���ʽ����a2��16��0��a+4��0��
���a��4��4���ᣩ��������Ϊb����b��4a��16��
�ʴ�Ϊ��4��16��
��2����P�˶�t�������ʾ����Ϊ4+3t����P���˶������д������·�����������������
������P�ڵ�B���ʱ�����У�4+3t��4��3��16��4��3t�������t��3��
������P�ڵ�B�Ҳ�ʱ�����У�4+3t��4��3��4+3t��16�������t��6��
�ʵ�ʱ��Ϊ3���6��ʱ����P����A�ľ����ǵ�P����B�ľ����3����
��3����P���˶���ʼ�����������д������·�����������������
����P��A��B֮��ʱ����4+4t+6��16+2t�����t��3��
����P��B��C֮��ʱ����4+4t��6��16+2t�����t��9��
��P�����C������Q��P���Ҳ�ʱ����12+2t+4t����40��4����6��36�����t��11��
��P�����յ�A��Q�����˶�����C���أ�����P���6ʱ����2t+6��24+36�����t��27��
�ʵ��˶�3�롢9�롢11���27��ʱ��P��Q����֮��ľ���Ϊ6��

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�����оٰ�������������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 6 |
��2�� | 30��x��35 | 8 |
��3�� | 35��x��40 | 16 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
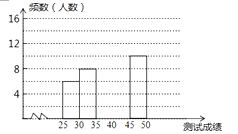
����ͼ��������и��⣺
��1�������a��ֵ����2�����Ƶ���ֲ�ֱ��ͼ����������
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
����Ŀ���������ϣ����꼶ij����ͬѧ������100�ײ��飬���ɼ�Ϊ15�룬�±�������С��8�������ijɼ���¼��������+����ʾ�ɼ�����15�룮
��0.8 | +1 | ��1.2 | 0 | ��0.7 | +0.6 | ��0.4 | ��0.1 |
�ʣ���1�����С�������Ĵ����Ϊ���٣�������ʣ�![]() ��
��
��2�����С��������ƽ���ɼ��Ƕ����룿