题目内容
【题目】阅读:圆是最完美的图形,它具有一些特殊的性质:同弧或等弧所对的圆周角相等,一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”,再利用圆的性质将问题进行转化,往往能化隐为显、化难为易。
解决问题:如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有_______个;
(2)若点P在y轴正半轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)设sin∠APB=m,若点P在y轴上移动时, 满足条件的点P有4个,求m的取值范围.
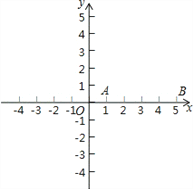
【答案】(1)无数;(2)(0, ![]() )或(0,
)或(0, ![]() );(3)0﹤m﹤
);(3)0﹤m﹤![]() .
.
【解析】试题分析:(1)已知点A、点B是定点,要使∠APB=30°,只需点P在过点A、点B的圆上,且弧AB所对的圆心角为60°即可,显然符合条件的点P有无数个.
(2)结合(1)中的分析可知:当点P在y轴的正半轴上时,点P是(1)中的圆与y轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P的坐标.
(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要∠APB最大,只需构造过点A、点B且与y轴相切的圆,切点就是使得∠APB最大的点P,由此即可求出m的范围.
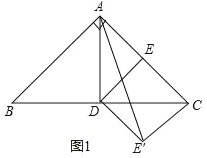
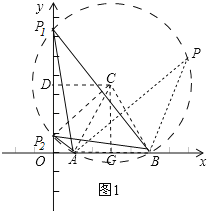
试题解析:解:(1)以AB为边,在第一象限内作等边三角形ABC,以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.
在优弧AP1B上任取一点P,如图1,则∠APB=![]() ∠ACB=
∠ACB=![]() ×60°=30°,∴使∠APB=30°的点P有无数个.
×60°=30°,∴使∠APB=30°的点P有无数个.
故答案为:无数.
(2)点P在y轴的正半轴上,过点C作CG⊥AB,垂足为G,如图1.
∵点A(1,0),点B(5,0),∴OA=1,OB=5,∴AB=4.
∵点C为圆心,CG⊥AB,∴AG=BG=![]() AB=2,∴OG=OA+AG=3.
AB=2,∴OG=OA+AG=3.
∵△ABC是等边三角形,∴AC=BC=AB=4,∴CG=![]()
=![]()
=2![]() ,∴点C的坐标为(3,2
,∴点C的坐标为(3,2![]() ).
).
过点C作CD⊥y轴,垂足为D,连接CP2,如图1.∵点C的坐标为(3,2![]() ),∴CD=3,OD=2
),∴CD=3,OD=2![]() .
.
∵P1、P2是⊙C与y轴的交点,∴∠AP1B=∠AP2B=30°.
∵CP2=CA=4,CD=3,∴DP2=![]() =
=![]() .
.
∵点C为圆心,CD⊥P1P2,∴P1D=P2D=![]() ,∴P1(0,2
,∴P1(0,2![]() +
+![]() ),P2(0,2
),P2(0,2![]() ﹣
﹣![]() ).
).
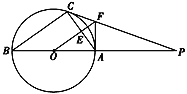
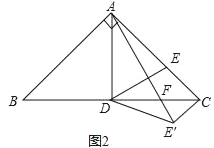
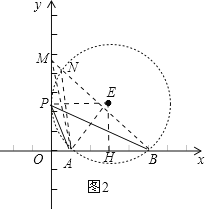
(3)当过点A、B的⊙E与y轴相切于点P时,∠APB最大.
理由:可证:∠APB=∠AEH,当∠APB最大时,∠AEH最大.由sin∠AEH=![]() 得:当AE最小即PE最小时,∠AEH最大.所以当圆与y轴相切时,∠APB最大.∵∠APB为锐角,∴sin∠APB随∠APB增大而增大,.
得:当AE最小即PE最小时,∠AEH最大.所以当圆与y轴相切时,∠APB最大.∵∠APB为锐角,∴sin∠APB随∠APB增大而增大,.
连接EA,作EH⊥x轴,垂足为H,如图2.∵⊙E与y轴相切于点P,∴PE⊥OP.
∵EH⊥AB,OP⊥OH,∴∠EPO=∠POH=∠EHO=90°,∴四边形OPEH是矩形,∴OP=EH,PE=OH=3,∴EA=3.sin∠APB=sin∠AEH=![]() ,∴m的取值范围是
,∴m的取值范围是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案