题目内容
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

【答案】(1)M(1,4);(2)点P的坐标为:(1,![]() )或(1,
)或(1,![]() );(3)E的运动的路径长为:
);(3)E的运动的路径长为:![]() .
.
【解析】
试题分析:(1)将解析式配成顶点式即可.(2)当点E与O重合时,设PN=m,过点C作CF⊥MN于F,由△ENP∽△PFC用相似比例建立方程解之即可.(3)找到左右两个极端位置即可.P在M点时,E在右边最运处,这个时候求出EN为对称轴右边的路径长度;E点在左侧时,设EN=y,PN=x,由△ENP∽△PFC列出比例方程,得到y关于x的二次函数,配方求出最大值,再加上右边路径长度即为总路径长度.
试题解析:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴M(1,4);
(2)当点E与O重合时,EN=1,设PN=m,
过点C作CF⊥MN,垂足为F,如图1,
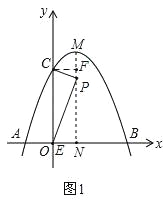
∵∠EPC=90°,
∴∠EPN+∠NEP=∠EPN+∠CPF=90°,
∴∠CPF=∠PEN,
∴△ENP∽△PFC
∴![]() ,即:
,即:![]() ,
,
解得:m=![]()
∴点P的坐标为:(1,![]() )或(1,
)或(1,![]() )
)
(3)①当点P与M重合时,如图2,
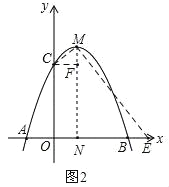
由△ENM∽△MFC可知,![]() ,
,
∴EN=4,
即当点P从M运动到F时,点E运动的路径长EN为4;
②当点P从F运动到N时,点E从点N向左运动到某最远点后,回到点N结束.如图3,
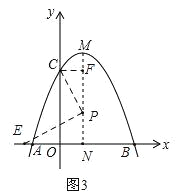
设EN=y,PN=x,
由△ENP∽△PFC可知,![]() ,即:
,即:![]() ,
,
∴y=![]() ,
,
当x=![]() 时,y有最大值,为
时,y有最大值,为![]() ;
;
∴E的运动的路径长为:![]() .
.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1

