Question

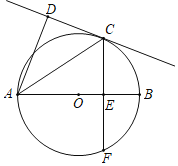
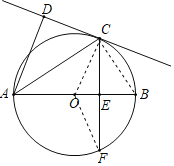
【题目】如图已知AB为⊙O的直径，CD切⊙O于C点，弦CF⊥AB于E点，连结AC．

（1）探索AC满足什么条件时，有AD⊥CD，并加以证明．

（2）当AD⊥CD，OA=5cm，CD=4cm，求△OCF面积．

Answer 1

【答案】（1）当AC满足平分∠BAD条件时，有AD⊥CD，见解析；（2）△OCF面积为12cm2．

【解析】

(1)当AD⊥CD时，∠ACD+∠DAC=90°．根据弦切角定理，∠ACD=∠B，而∠B+∠BAC=90°，因此可得出∠BAC=∠CAD，因此AC需要满足的条件是AC是∠BAD的平分线；

(2)关键是求CF、OE的长，可先根据角平分线的性质，求出CE的长，进而求得CF的长，然后在直角三角形COE中求出OE的长，即可根据三角形面积公式求得△OCF面积．

(1)当AC满足平分∠BAD条件时，有AD⊥CD，

证明如下：连接BC，

则∠ACB=90°，即∠ABC+∠BAC=90°，

∵CD是圆O的切线，

∴∠ACD=∠ABC，

∵AC平分∠BAD，

∴∠BAC=∠CAD，

∴∠CAD+∠ACD=90°，

即∠ADC=90°，AD⊥CD；

(2)连结OC、OF．

∵CD切⊙O于C点，

∴OC⊥CD．

∵AD⊥CD，

∴OC∥AD，

∴∠OCA=∠DAC，

∵OA=OC，

∴∠OCA=∠OAC，

∴∠OAC=∠DAC．

∴AC平分∠BAD，

∴CD=CE，

∵OA=5，CD=4，

∴OC=OA=5，CE=4，

∵CF⊥AB，

∴CF=2CEOE===3，

∴CF=2×4=8，CF×OE÷2=8×3÷2=12，

故△OCF面积为12cm2．