ЬтФПФкШн
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2Љ2axЉ2ЃЌгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌAЃЈЉ2ЃЌ0ЃЉ
ЃЈ1ЃЉжБНгаДГіЃКaЃНЁЁ ЁЁ
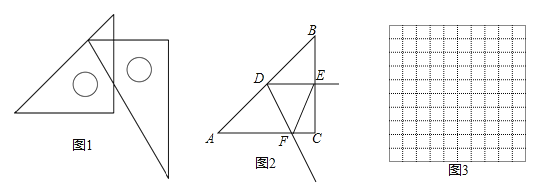
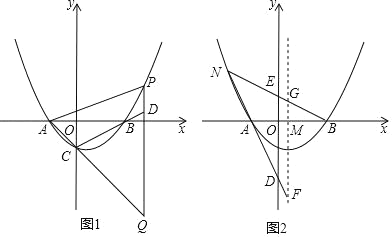
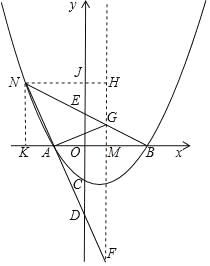
ЃЈ2ЃЉШчЭМ1ЃЌЕуPдкЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпНЛCBЕФбгГЄЯпгкЕуDЃЌНЛACЕФбгГЄЯпгкЕуQЃЌЕБЁїQAPгыЁїQCDЯрЫЦЪБЃЌЧѓPЕуЕФзјБъЃЛ
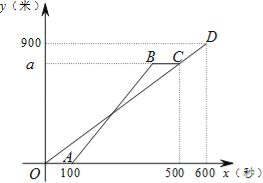
ЃЈ3ЃЉШчЭМ2ЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуMЃЌNЮЊЕкЖўЯѓЯоФкХзЮяЯпЩЯЕФвЛЕуЃЌжБЯпNAЃЌNBЗжБ№НЛyжсгкDЃЌEСНЕуЃЌЗжБ№НЛХзЮяЯпЕФЖдГЦжсгкFЃЌGСНЕуЃЎ
ЂйЧѓtanЁЯFAMЉtanЁЯGAMЕФжЕЃЛ
ЂкШє![]() ЃЌЧѓNЕуЕФзјБъЃЎ
ЃЌЧѓNЕуЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕуPЕФзјБъЮЊЃЈ6ЃЌ4ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйtanЁЯFAMЉtanЁЯGAMЃН![]() ЃЛЂкЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ
ЃЛЂкЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAДњШыХзЮяЯпМДПЩЃЎ
ЃЈ2ЃЉЯрЫЦЗжСНжжЧщПіЃЌвЛжжЪЧAPЁЮCDЃЌИљОнСНжБЯпЦНааkЯрЕШЃЌдйДњШыЕуAОЭПЩвдЧѓГіДЫЪБжБЯпAPЕФНтЮіЪНЃЌКЭХзЮяЯпСЊСЂОЭПЩвдЧѓГіЕуPЕФзјБъЃЛСэвЛжжИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЃЌСаЗНГЬЧѓНтМДПЩЃЎ
ЃЈ3ЃЉЂйЩшЕуNЕФзјБъЃЌБэЪОЯпЖЮГЄЖШЃЌСаБШжЕЫуГіЪ§жЕМДПЩЃЎЂкзЊЛЛЬтИЩжаЕФБШжЕЃЌАбаБЯпЕФБШжЕзЊЛЛЮЊЫЎЦНЯпЕФБШжЕЃЌБэЪОЯпЖЮГЄЖШЃЌСаЪНЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉНЋAЃЈЉ2ЃЌ0ЃЉДњШыХзЮяЯпжаЃЌЕУ
0ЃН4a+4aЉ2ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СюyЃН0ЃЌНтЕУx1ЃНЉ2ЃЌx2ЃН4ЃЌ
ЁрBЃЈ4ЃЌ0ЃЉЃЌ
СюxЃН0ЃЌyЃНЉ2ЃЌ
ЁрCЃЈ0ЃЌЉ2ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊyЃНkx+bЃЌДњШыЕуAЁЂCЃЌЕУЃК![]()
НтЕУ![]()
ЁрyЃНЉxЉ2ЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊyЃНk1 x+b1ЃЌДњШыЕуЕуBЁЂCЃЌЕУЃК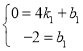
НтЕУ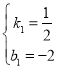
ЁрyЃН![]() xЉ2ЃЌ
xЉ2ЃЌ
ЩшЕуPЕФКсзјБъЮЊmЃЌдђзнзјБъЮЊ![]() ЃЌ
ЃЌ
дђЕуDЃЈmЃЌ ![]() mЉ2ЃЉЃЌQЃЈmЃЌЉmЉ2ЃЉЃЌ
mЉ2ЃЉЃЌQЃЈmЃЌЉmЉ2ЃЉЃЌ
PQЃН![]() ЃЌ
ЃЌ
DQЃН![]() ЃЌ
ЃЌ
AQЃН![]() ЃЌ
ЃЌ
CQЃН![]() ЃЌ
ЃЌ
ЂйЕБAPЁЮCDЪБЃЌЁїAPQЁзЁїCDQЃЌ
ЩшжБЯпAPЕФНтЮіЪНЮЊyЃН![]() x+b3ЃЌ
x+b3ЃЌ
ДњШыЕуAЃЌ0ЃН![]() ЁСЃЈЉ2ЃЉ+b3ЃЌНтЕУb3ЃН1ЃЌ
ЁСЃЈЉ2ЃЉ+b3ЃЌНтЕУb3ЃН1ЃЌ
ЁрyЃН![]() x+1ЃЌ
x+1ЃЌ
Сю![]() x+1ЃН
x+1ЃН![]() x2Љ
x2Љ![]() Љ2ЃЌ
Љ2ЃЌ
НтЕУx1ЃНЉ2ЃЌx2ЃН6ЃЌ
ЕБxЃН6ЪБЃЌyЃН4ЃЌ
ЁрPЃЈ6ЃЌ4ЃЉЃЎ
ЂкЕБЁЯAPQЃНЁЯQCDЪБЃЌЁїAPQЁзЁїDCQЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр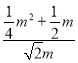 ЃН
ЃН
НтЕУm1ЃНЉ2ЃЈЩсЃЉЃЌm2ЃН![]() ЃЌ
ЃЌ
ЕБxЃН![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЌ
ЃЌ
ЁрPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃЈ6ЃЌ4ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉЂйЙ§ЕуNзїNKДЙжБxжсгкЕуKЃЌ
ЩшЕуNЕФзјБъЮЊЃЈnЃЌ![]() n2Љ
n2Љ![]() nЉ2ЃЉЃЌ
nЉ2ЃЉЃЌ
дђNKЃН![]() n2Љ
n2Љ![]() nЉ2ЃЌAKЃНЉ2ЉnЃЌBKЃН4ЉnЃЌ
nЉ2ЃЌAKЃНЉ2ЉnЃЌBKЃН4ЉnЃЌ
tanЁЯFAMЃНtanЁЯNAK=![]() ЃН
ЃН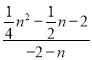 ЃЌ
ЃЌ
tanЁЯGAMЃНtanЁЯGBK=![]() ЃН
ЃН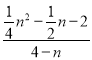 ЃЌ
ЃЌ
ЁрtanЁЯFAMЉtanЁЯGAMЃН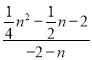 -
-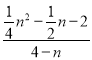 =
=![]() ЃЎ
ЃЎ
ЂкЁп![]() ЃЌЁїNEDЁзЁїNGFЃЌ
ЃЌЁїNEDЁзЁїNGFЃЌ
Ёр![]() ЃЌ
ЃЌ
Й§ЕуNЯђХзЮяЯпЕФЖдГЦжсзїДЙЯпЃЌЗжБ№НЛyжсКЭЖдГЦжсгкЕуJЁЂHЃЌ
ЁрЁїNJEЁзЁїNHGЃЌ
Ёр![]() ЃЌ
ЃЌ
NJЃНЉnЃЌNHЃН1ЉnЃЌ
Ёр4ЃЈ1ЉnЃЉЃНЉ5nЃЌ
НтЕУnЃНЉ4ЃЌ
ЕБxЃНЉ4ЪБЃЌyЃН4ЃЌ
ЁрЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ

 зжДЪОфЖЮЦЊЯЕСаД№АИ
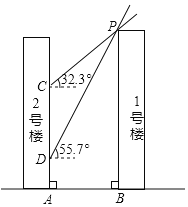
зжДЪОфЖЮЦЊЯЕСаД№АИЁОЬтФПЁПдкЪ§бЇЛюЖЏПЮЩЯЃЌРЯЪІЬсГіСЫвЛИіЮЪЬтЃКАбвЛИБШ§НЧГпШчЭМАкЗХЃЌжБНЧШ§НЧГпЕФСНЬѕжБНЧБпЗжБ№ДЙжБЛђЦНааЃЌ60ЁуНЧЕФЖЅЕудкСэвЛИіШ§НЧГпЕФаББпЩЯвЦЖЏЃЌдкетИідЫЖЏЙ§ГЬжаЃЌгаФФаЉБфСПЃЌФмбаОПЫќУЧжЎМфЕФЙиЯЕТ№ЃП
аЁСжбЁдёСЫЦфжавЛЖдБфСПЃЌИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдЫќУЧжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁСжЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЛГіМИКЮЭМаЮЃЌУїШЗЬѕМўКЭЬНОПЖдЯѓЃЛ
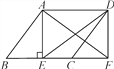
ШчЭМ2ЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=BC=6cmЃЌDЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЩфЯпDEЁЭBCгкЕуEЃЌЁЯEDF=60ЁуЃЌЩфЯпDFгыЩфЯпACНЛгкЕуFЃЎЩшBЃЌEСНЕуМфЕФОрРыЮЊxcmЃЌEЃЌFСНЕуМфЕФОрРыЮЊycmЃЎ
ЃЈ2ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщжЕЃЌШчЯТБэЃК
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
ЃЈЫЕУїЃКВЙШЋБэИёЪБЯрЙиЪ§ОнБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ3ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБЁїDEFЮЊЕШБпШ§НЧаЮЪБЃЌBEЕФГЄЖШдМЮЊ cmЃЎ