题目内容
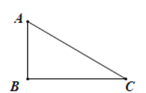
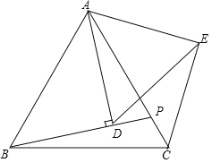
【题目】如图,![]() 为等边三角形,点
为等边三角形,点![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线段,垂足为点
的垂线段,垂足为点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 为
为![]() 的中点;
的中点;
(3)在(2)的条件下,若![]() 的边长为1,直接写出
的边长为1,直接写出![]() 的最大值.
的最大值.
【答案】(1)证明见解析;(2)证明见解析;(3)1.
【解析】
(1)由等边三角形的性质和旋转的性质可得∠DAB=∠CAE,AB=AC,AD=AE,即可证△ADB≌△AEC,可得BD=CE;
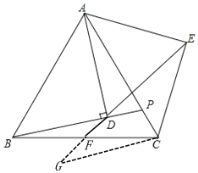
(2)过点C作CG∥BP,交EF的延长线于点G,由等边三角形的性质和全等三角形的性质可得CG=BD,∠BDG=∠G,∠BFD=∠GFC,可证△BFD≌△CFG,可得结论;
(3)由题意可证点A,点F,点C,点E四点在以AC为直径的圆上,由直径是圆的最大弦可得EF的最大值.
证明:(1)∵将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如图,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() 是
是![]() 中点.
中点.
(3)如图,连接![]() ,
,
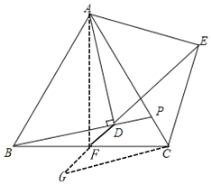
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点在以
四点在以![]() 为直径的圆上,
为直径的圆上,
∴![]() 最大为直径,
最大为直径,
即最大值为1.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案【题目】某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分):整理、分析过程如下,请补充完整.
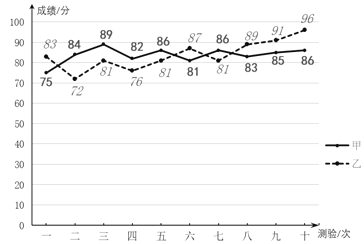
(1)按如下分数段整理、描述这两组数据:
成绩x 学生 | 70≤x≤74 | 75≤x≤79 | 80≤x≤84 | 85≤x≤89 | 90≤x≤94 | 95≤x≤100 |
甲 | ______ | ______ | ______ | ______ | ______ | ______ |
乙 | 1 | 1 | 4 | 2 | 1 | 1 |
(2)两组数据的极差、平均数、中位数、众数、方差如下表所示:
学生 | 极差 | 平均数 | 中位数 | 众数 | 方差 |
甲 | ______ | 83.7 | ______ | 86 | 13.21 |
乙 | 24 | 83.7 | 82 | ______ | 46.21 |
(3)若从甲、乙两人中选择一人参加知识竞赛,你会选______(填“甲”或“乙),理由为______.