题目内容
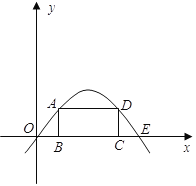
【题目】如图:矩形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线![]() 上,矩形的顶点均为动点,且矩形在抛物线与
上,矩形的顶点均为动点,且矩形在抛物线与![]() 轴围成的区域里。
轴围成的区域里。
(1)设A点的坐标为(![]() ,
, ![]() ),试求矩形周长
),试求矩形周长![]() 关于变量
关于变量![]() 的函数表达式;
的函数表达式;
(2)是否存在这样的矩形,它的周长为9,试证明你的结论。
【答案】(1)![]() (2)不存在,证明见解析.
(2)不存在,证明见解析.
【解析】试题分析:(1)根据抛物线的解析式令y=0,可求出抛物线与x轴两交点的坐标,因为A点的坐标为(x,y),则B点坐标为(x,0),即OB=x,由抛物线的对称性可知EC=x,则BC=4-2x,再根据矩形的面积公式可求出矩形周长p关于变量x的函数表达式;
(2)先假设符合条件的矩形存在,把9代入(1)所求的矩形周长公式,根据一元二次方程判别式的情况判断出方程解的情况即可判断P是否存在.
试题解析:(1)令![]() =0
=0
得:x1=0,x2=4.
则抛物线与坐标轴两交点的坐标为O(0,0)、E(4,0)
设OB=x,由抛物线的对称性可知EC=x,则BC=42x.
P=2(42x+y)=2(42x ![]() )
)
P=![]()
(2)不存在。
若存在周长为9的矩形ABCD,则![]() =9
=9
①4x24x+3=0,△=1648<0
方程①无实数根,即不存在这样的矩形。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目