题目内容
【题目】
(1)已知:如图1,等腰直角三角形ABC中,∠B=90°,AD是∠BAC的外角平分线,交CB边的延长线于点D.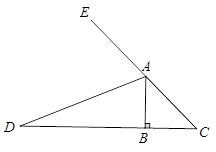
图1
求证:BD=AB+AC
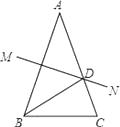
(2)对于任意三角形ABC,∠ABC=2∠C,AD是∠BAC的外角平分线,交CB边的延长线于点D,如图2,请你写出线段AC、AB、BD之间的数量关系并加以证明.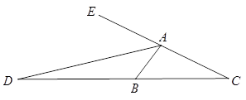
【答案】
(1)解:在AE于上截取AF=AB,连接DF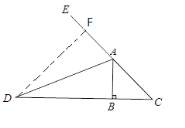
∵AD是∠BAC的外角平分线
∴∠DAF=∠DAB
在△ADF和△ADB中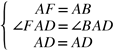
∴△ADF≌△ADB
BD=DF;∠DFA=∠DBA=90°
又∵等腰直角三角形ABC中,∠BAC=∠C=45°
∴FAD=135°
∴∵FDC=45°=∠C
∴DF=FC
∴BD=CF=AC+AF
BD=AB+AC
(2)解:DB=AB+AC理由如下:
在AE上截取AF=AB,连接DF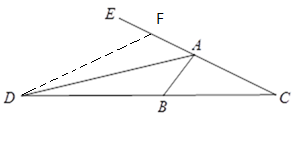
∵AD是∠BAC的外角平分线
∴∠FAD=∠BAD
在△FAD和△BAD中,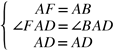
∴△FAD≌△BAD
∠ADF=∠ADB;BD=DF
∠AFD+∠EFD=∠ABD+∠ABC=180°
∴∠EFD=∠ABC
∵∠ABC=2∠C
∴∠EFD=2∠C
∵∠EFD=∠FDC+∠C
∴DF=CF
BD=CF=AF+AC
∴DB=AB+AC
【解析】(1)做辅助线,由外角平分线易得△ADF≌△ADB,再由等腰直角三角形性质易得DF=FC=BD,最终得证DB=AB+AC;
(2)类比(1)中的方法,在证DF=CF时利用所给条件∠ABC=2∠C,可证,最终得证DB=AB+AC

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目