题目内容
【题目】如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF=（ ）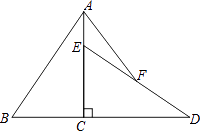
A.4
B.5
C.4 
D.6
【答案】B
【解析】如图所示：取CE的中点G，连接FG．
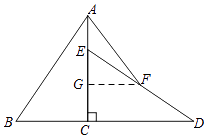
由旋转的性质可知：CE=BC=4，CD=AC=6，
∴AE=2，GE=2．
∴AG=4．
∵点G为CE的中，点F为ED的中点，
∴GF= 
CD=3，GF∥CD．
又∵CD⊥AC，
∴FG⊥AC．
在Rt△AGF中，依据勾股定理可知AF= 
=5．
所以答案是：B．
【考点精析】通过灵活运用勾股定理的概念和旋转的性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了即可以解答此题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
