Question

【题目】细心观察图，认真分析各式，然后解答问题：

；

；

；

（1）请用含（为正整数）的等式表示上述交化规律：______；

（2）观察总结得出结论：直角三角形两条直角边与斜边的关系，用一句话概括为：______；

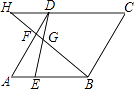
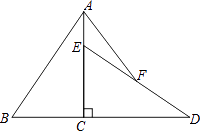
（3）利用上面的结论及规律，请在图中作出等于的长度；

（4）若表示三角形面积，，，，计算出的值．

Answer 1

【答案】（1）；（2）直角边的平方和等于斜边的平方；（3）见解析；（4）．

【解析】

（1）观察已知各式，归纳总结规律即可得；

（2）根据等式和图形即可得；

（3）先作的垂线，再在垂线上截取，连接，可得，同理可作出点，连接即为所求；

（4）先分别求出的值，再归纳总结出一般规律得出的值，从而可得的值，然后代入求和即可．

（1）观察已知各式可得，各式的变化规律为

故答案为：；

（2）结合等式和图形可得，直角三角形两条直角边与斜边的关系为：直角边的平方和等于斜边的平方

故答案为：直角边的平方和等于斜边的平方；

（3）先作的垂线，再在垂线上截取，连接，即可得，同理可作点，连接，则即为所求，如图所示：

（4）

归纳类推得：

当时，

则

．