题目内容
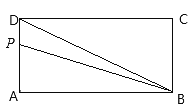
【题目】如图,长方形ABCD中,AB=2cm,BC=4cm,点P按照顺时针方向由点A运动到点D,设点P运动的路程为![]() 图中点P、B、D围成的图形的面积为
图中点P、B、D围成的图形的面积为![]()
(1)写出点P、B、D围成的图形的面积![]() 与
与![]() 之间的关系式和自变量
之间的关系式和自变量![]() 的取值范围;
的取值范围;
(2)当![]() 取何值时,点P、B、D围成的图形的面积等于
取何值时,点P、B、D围成的图形的面积等于![]() ?
?
【答案】(1)y=4-x(0≤x≤4);(2)x=1
【解析】
(1)当点P由点A运动到点D,求出DP的长,根据三角形面积公式计算即可;
(2)把y=3代入式子即可得出答案.
解:(1)∵四边形ABCD是长方形,
∴AD=BC=4,AB=CD=2,
∵DP=AD-AP,
∴DP=4-x,
当点P在AD上时,即0≤x≤4时,
y=![]() ×(4-x)×2=4-x;
×(4-x)×2=4-x;
(2)y=4-x=3
x=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目