Question

【题目】如图，是的直径，是的切线，是切点，与交于点．

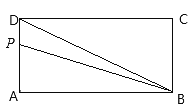
（1）如图①，若，，求的长；

（2）如图②，若为的中点，求证：直线是的切线．

Answer 1

【答案】（1）；（2）见解析；

【解析】

（1）首先根据切线的性质判定∠BAP=90°；然后在直角三角形ABP中利用三角函数的定义求得AP的长度；
（2）连接OC，OD、AC构建全等三角形△OAD≌△OCD，然后利用全等三角形的对应角相等推知∠OAD=∠OCD=90°，即OC⊥CD．

（1）解：∵AB是⊙O的直径，AP是⊙O的切线，
∴AB⊥AP，
∴∠BAP=90°；
又∵AB=2，∠P=30°，
∴AP= ；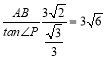
（2）证明：如图，连接OC，OD、AC．
∵AB是⊙O的直径，
∴∠ACB=90°（直径所对的圆周角是直角），
∴∠ACP=90°；
又∵D为AP的中点，
∴AD=CD（直角三角形斜边上的中线等于斜边的一半）；
在△OAD和△OCD中，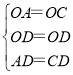
，
∴△OAD≌△OCD（SSS），
∴∠OAD=∠OCD（全等三角形的对应角相等）；
又∵AP是⊙O的切线，A是切点，
∴AB⊥AP，
∴∠OAD=90°，
∴∠OCD=90°，即直线CD是⊙O的切线．