题目内容
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
【答案】
(1)解:y=(x﹣20)w
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
∴y与x的函数关系式为:
y=﹣2x2+120x﹣1600
(2)解:y=﹣2x2+120x﹣1600
=﹣2(x﹣30)2+200,
∴当x=30时,y有最大值200,
∴当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)解:当y=150时,可得方程:
﹣2(x﹣30)2+200=150,
解这个方程,得
x1=25,x2=35,
根据题意,x2=35不合题意,应舍去,
∴当销售价定为25元/千克时,该农户每天可获得销售利润150元.
【解析】(1)根据每天的销售利润=销售量![]() (售价-进价),列出函数解析式即可。
(售价-进价),列出函数解析式即可。
(2)根据(1)中的函数解析式求出顶点坐标,即可得出结论。
(3)根据每天获得销售利润=150,建立方程,解方程求解,再根据销售价不高于每千克28元,确定售价即可。

 名校课堂系列答案
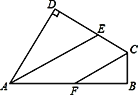
名校课堂系列答案【题目】已知:如图所示,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,AE//CF.
(1)说明:CF平分∠BCD;
(2)作△ADE的高DM,若AD=8,DE=6,AE=10,求DM的长。
【题目】某公司计划购买若干台打印机,现从两家商场了解到同一种型号的打印机报价均为1000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠15% |
乙商场 | 每台优惠10% |
(1)设公司购买![]() 台打印机,选择甲商场时,所需费用为
台打印机,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现从甲乙两商场一共买入10台打印机,已知甲商场的运费为每台15元,乙商场的运费为每台20元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台打印机,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?